Deep Image Compression via End to End Learning

07 Jul 2018 • Briefs • Machine Learning

본 논문은 ariv에 올라온 논문으로 2018년 6월 5일에 올라온 가장 최신의 논문이다.

요약 및 Introduction

해당 논문은 가장 최신의 정지영상 압축을 논한 것으로서 HEVC Intra인 BPG 보다 월등한 성능 (MSSSIM - BDrate로 7.81% ~ 19.1% 성능을 내었다. with respect to Kodak and ETH data set)을 보여주었다. 특징은 다음과 같다.

  • 3 단계 Downsampling과 Upsampling을 사용하였다.
    • Upsampling은 Super Resolution에 사용된 CNN 구조를 그대로 사용하였다.
  • RD Optimization을 반영한 Perceptual Loss Function을 사용하였다.
  • ReLu 함수대신 PReLu (Paeametric Rectified Linear Unit) 를 사용하였다.
  • Entropy Coding Tool로 PAQ를 사용하였다.
    • PAQ의 압축 성능이 매우 뛰어나 보인다. 적어도 JPEG의 2배 이상이다.
    • 사실, 여기에서 모든 성능이 나오는 것은 아닌지 의심된다.
  • Adversarial Loss를 고려하여 Wasserstein GAN (WGAN)[1]을 사용하였다.

End to End Learning Frame work

  • Down sampling
    • Stride-2 $4 \times 4$ Convolution Layer
  • Up samling : Super Resolution에서 사용하는 방식 그대로이다.
    • $3 \times 3$ Kernel을 일반적으로 사용한다.
    • $5 \times 5$ Kernel은 First/Last Layer에서 사용한다.
  • pReLu \(f(x) = \max(0,x) + w \cdot \min(0, x) \\ f'(x) = \begin{cases} 1 & x > 0 \\ 0 & x = 0 \\ w & x <0 \end{cases}\)

Quantization and Entropy Coding

간단한 Scalar Quantization을 사용한다. \(X_Q = Round\left( X_E \cdot (2^Q - 1) \right)\) where $X_E \in (0,1)$ 은 Feature Map (fMAP)의 Coefficient이다. (Sigmoid 함수 출력), $Q$는 Quantization Level 이며 6으로 세팅되어 있다.

  • Binary Coding을 위해 이렇게 만들어진 값에 PAQ를 적용한다.
  • De-quantization은 \({X'}_E = \frac{X_Q}{2^Q - 1}\)
  • Back propagation에서는 Round Function을 생략한다.

Rate Estimation

Rate loss $L_R$은 다음과 같이 정의된다. \(L_R = - \mathbb{E}[\log_2 P_q]\) where $L_R$ 은 Bottleneck layer에서 fMaps의 Entropy approximation이다. Qunatization 의 미분은 거의 0이기 때문에, Discrete 함수인 $P_q$의 Piecewise 선형근사를 사용하여 이것을 연속 및 미분 가능함수로 만들어야 한다.

  • Balle[2]는 유사한 아이디어를 자신의 논문에 제시한 바 있다.

Network Training

  • 데이터의 크기 $128 \times 128$
  • 데이터의 갯수 80000 patches

  • Objective Function \(L = \frac{1}{N}\sum_{n=1}^N \| Y_n - x_n \|^2 + \lambda L_R\) where $X_n$ Input Image, $Y_n$ Decoded Image, N is Batch size (i.e. 80000)

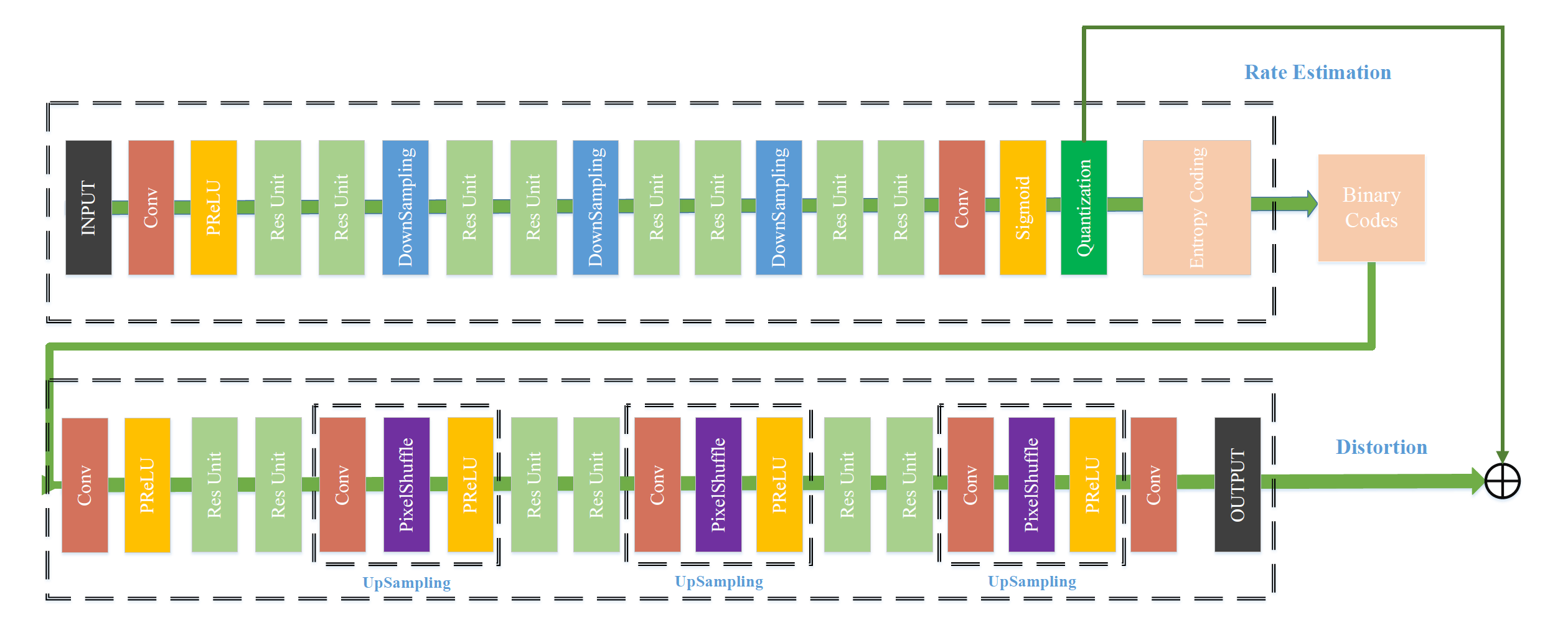
  • Network의 구조는 다음과 같다. fig_deep_01

Visual Enhancement

Perception Loss

  • Feature Extraction을 위해 31-Layer의 VGGnet을 사용[2]
  • Perceptual Loss \(L_{\text{perceptual}} = \frac{1}{N} \sum_{n=1}^N \| \Psi(Y_n) - \Psi(X_n) \|^2\)
  • $\Psi$ is the VGGnet to compute the feature.

Adversarial Loss

  • Discriminator neural network $D$ 는 image가 진짜인지 Fake인지를 가려낸다.
  • 본 논문에서는 일반적인 DCGAN을 Wasserstein GAN으로 구현한다.
    • 보다 빠른 수렴과 안정성을 나타낸다.
  • WGAN은 Earth-Move divergence 혹은 Wasserstrein Metric를 사용한다.
  • Reconstructed Image가 높은 확률(?)을 가질 수 잇도록 다음과 같이 정의한다. \(L_{\text{generator}} = -D(Y_n)\)

  • 한편 Discereminator Loss는 다음과 같이 정의한다. \(L_{\text{Discereminator}} = D(Y_n) - D(X_n) + \beta L_{\text{Penalty}}\) 여기서 $D$는 Discreminative Neural Network 이며 $L_{\text{penalty}}$는 improved WGAN에서 언급되는 Penalty term이며 $\beta$는 parameter로서 10이다.

  • 최종적인 Loss Function은 다음과 같다. \(L_{\text{final}} = L_2 + \lambda_1 L_R + \lambda_2 L_{\text{perceptual}} + \lambda_3 L_{\text{generator}}\) with $\lambda_2 = 0.003$, $\lambda_3 = 0.0001$.

Performance and Conclusion

  • Kodak Data 실험 결과는 평균 약 7.81% BPG에 대하여 MSSSIM-BD-rate 상승을 보여준다.
  • CLIC test data set 에서는 33.54 ~9.65% MSSSIM-BD-rate 상승을 보여준다.

My Comment

  • BPG가 동일한 Entopy Coding Scheme을 사용하였다면 매우 뛰어난 결과이다.
  • 그럼에도 양자화 부분에 대하여는 간단한 접근을 취했다.
  • 이것을 Inter Frame에 접근 시킨다면 결과는 알 수 없다.
  • WGAN 에 대하여 알아볼 필요성이 있음

Figure of Simulation Result

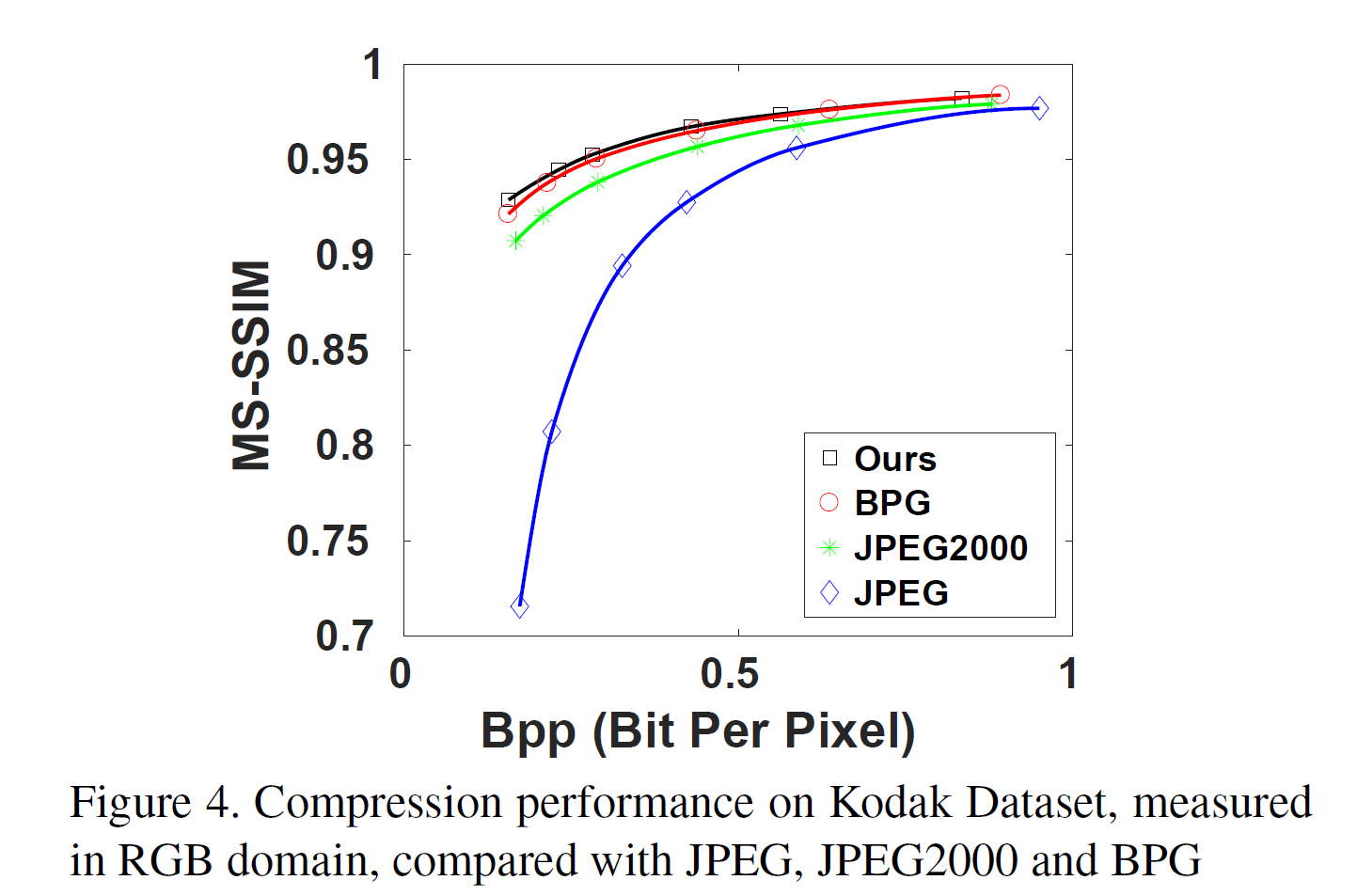
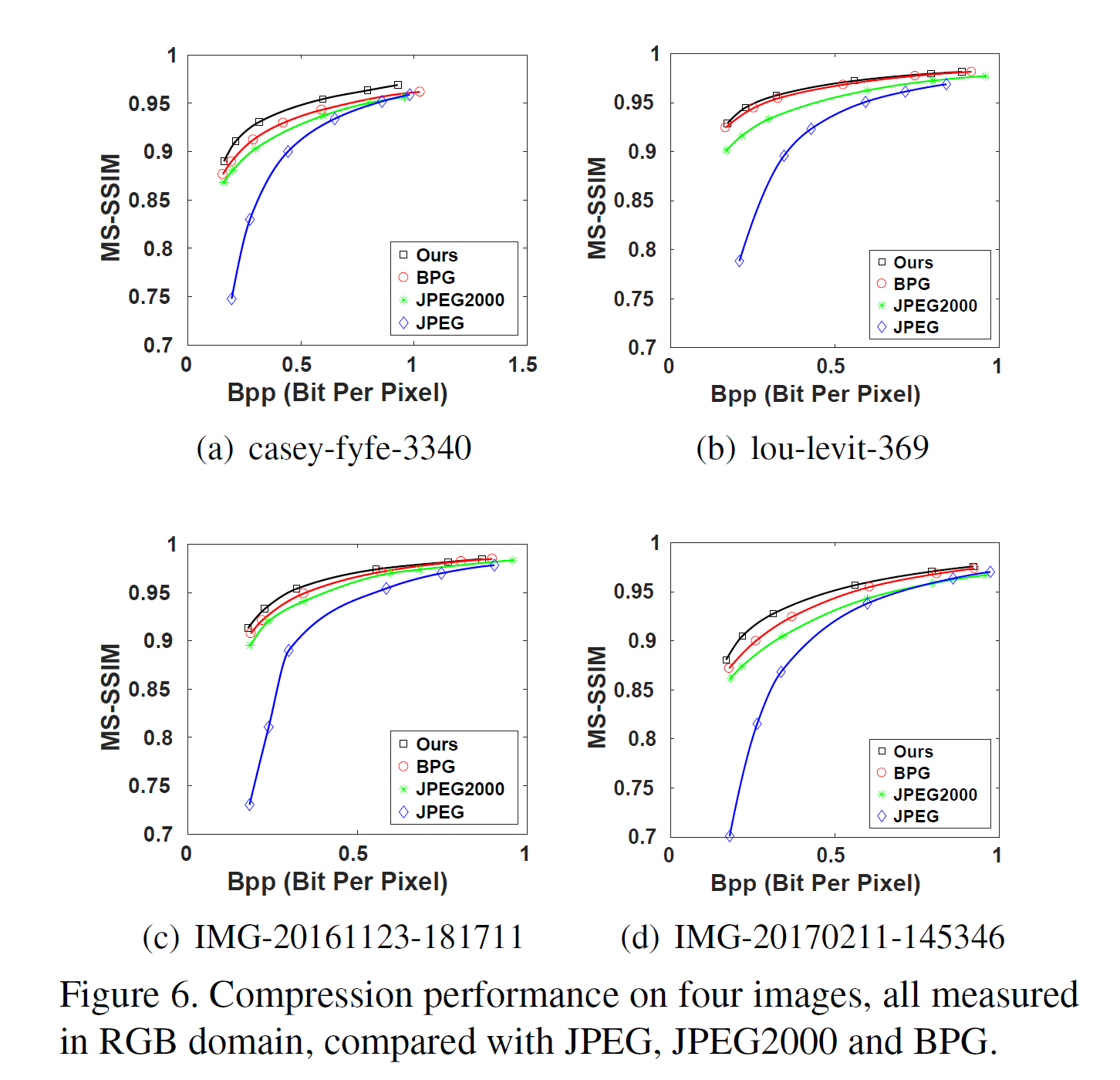
fig_deep_02 fig_deep_03

Reference

[1] M. Arjovsky, S. Chintala, and L. Bottou. Wasserstein gan. arXiv preprint arXiv:1701.07875, 2017.

[2] K. Simonyan and A. Zisserman. Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556, 2014.

 Machine-Learning

Comments

Related Posts