- Norm
- Open Set and Closed Set
- Sequence
- Limit Point and Accumulation points
- Theorem 1.
- Definition 7. Monotone Decreasing Sequence
- Theorem 2
- Continuity and Uniform Continuity
- Derivative
Norm
A Norm in $\mathbb{R}^n $ is a function \(|| \cdot || : \mathbb{R}^n \rightarrow \mathbb{R}_{+}\)
- $\left |x \right | = 0$ iff $x = 0$
- $\left | \lambda x \right | = | \lambda | \left | x \right | \;\;\;\forall \lambda \in \mathbb{R}, \; x \in \mathbb{R}^n $
- $\left | x + y \right | \leq \left |x\right | + \left |y\right | \;\;\; \forall x, y \in \mathbb{R}^n $
Open Set and Closed Set
Definition 1. Open ball
$\forall x \in \mathbb{R}^n$ and $\rho > 0$, by
\(B^{o}(x, \rho) = \{ z \in \mathbb{R}^n | ||z - x || < \rho \}\) we denote an open ball with radius $\rho$.
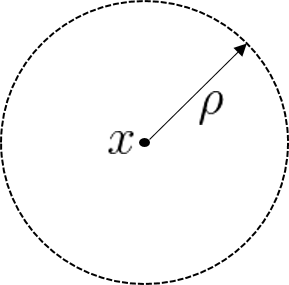 Figure 1. Open Ball
Figure 1. Open Ball
Definition 2. Open Set
A Set $Z \subset \mathbb{R}^n$ is said to be a Open, \(if \; \forall x \in Z \;\; and \;\; \exists \rho > 0, \;\; \exists B^{o}(x,\rho) \subset Z\)
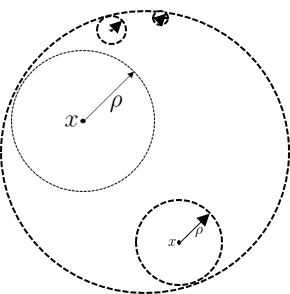 Figure 2. Open Set
Figure 2. Open Set
Example
An open ball $B^{o}(x, \rho)$ is am open set.
Definition 3. Closed Set
A set $Z \subset \mathbb{R}^n$ is said to be ** Closed (Set) **, if its complement in $\mathbb{R}^n$ is open.
- 즉, $Z^{c}$ 가 Open Set 이면 $Z$ 는 Close Set.
Definition 4. Compact
A set $Z \subset \mathbb{R}^n$ is said to be ** Compact **, if ** every open covering of $Z$ has a ++finite++ open covering **
Note
A Compact set in $\mathbb{R}^{n}$ is closed and bounded.
- 모든 원소의 Open subset 으로 Infinite 하게 Cover되는 Open Set의 여집합이면 Closed Set 이면서 Finite하게 Cover 된다.
Example
Is a set $(0, 1]$ closed?
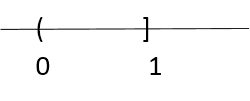
Set $u_i = (0, 1 - \frac{1}{i}]$. The set $(0, 1]$ is **OPEN ** since $\bigcup_{i=0}^{\infty} u_i \supset (0, 1] $ through $\bigcup_{i=0}^{\infty} u_i \supseteq (0, 1 - \epsilon]$.
- Finite가 아니므로 Open
Sequence
A Sequence is a function from $\mathbb{N}$ to $\mathbb{R}^n$ such that
\[\{x_i\}^{\infty}_{i=1}\]A Subsequence of \(\{ x_i \}^{ \infty }_{ i=1 }\) is a set \(\{ x_i \}_{i \in \mathbb{K}}\) where $\mathbb{K} \subset \mathbb{N}$ has an infinite number of elements.
Limit Point and Accumulation points
Definitioon 5. Limit Point (Important!)
A sequence ${x_i}_{i \in \mathbb{N}}$ is said to be converge to $\hat{x}$,
\[if \;\; \lim_{i \rightarrow \infty}\left \| x_i - \hat{x} \right \| = 0.\]or, (다음 정의가 더 중요하다.)
\[\forall \epsilon > 0 \;\; and \;\; \exists i_0 \in \mathbb{N}, \;\; \exists \left\| x_i - \hat{x}\right\| < \epsilon , \;\; \forall i \geq i_0\]The point $\hat{x}$ is called a limit point.
Definition 6. Accumulation point
A point $ x^* $ is called an accumulation point if, There exists an infinite subsequence , ${x_i }_{i \in \mathbb{K}}$ such that $x_i \overset{\mathbb{K}}{\rightarrow} x^{*}$ 즉,
\[\lim_{\overset{i \rightarrow \infty}{ i \in \mathbb{K}}} \left\| x_i - x^* \right\| = 0\]- 처음부터 시작하여 무한하면 Limit Point, 임의의 시작점에서 무한하면 Accumulation point
HW. 가산집합(countable set)과 가부번 집합(de-numerator set)에 대하여 알아올 것.
Theorem 1.
$Z \subset \mathbb{R}$ is closed iff a sequence ${x_i}_{i \in \mathbb{N}} \subset Z$ converges to $\hat{x}$ (i.e. $x_i \rightarrow \hat{x}$) then $\hat{x} \in Z$.
proof
Sufficient
Suppose that $\hat{x} \notin Z \Rightarrow \hat{x} \in Z^c$. Since $\exists \rho > 0$ such that $B^o(\hat{x}, \rho) \subset Z^c$, and, by assumption, $x_i \rightarrow \hat{x} \;\; for \;\;\rho > 0$, $\exists i_0 \in \mathbb{N}$, such that $\left| x_i -\hat{x} \right| < \rho, \;\; \forall i \geq i_0$. i.e. $x_i \in B^o(\hat{x}, \rho) \subset Z^c, \;\; \forall i \geq i_0$ (Open Set의 정의에 따라 이는 당연, 즉, $x_i \in Z^c$).
However, by assumption, $x_i \in Z$. 따라서 이는 가정에 모순이다.
Necessity
Suppose that $Z$ is not close (i.e. open), it means that $Z^c$ is not open (i.e. close). ,and $\exists \hat{x} \in Z^c$ (결론이 반대라고 가정하면..) such that $\forall \rho > 0, B^o (\hat{x}, \rho) \nsubseteq Z^c $ (i.e. $B^o (\hat{x}, \rho) \cap Z^C = \varnothing$). (가정과 결론이 반대인 경우가 성립한다고 가정하면) Let $\rho_i = \frac{1}{i}$, and pick $x_i \in B^o (\hat{x}, \rho_i) \cap Z$, then $x_i \rightarrow \hat{x}, \;\; x_i \in Z, \;\; \forall i$. However, $\hat{x} \in Z^c$, and it is contradict to the assumption.
[Q.E.D]
Definition 7. Monotone Decreasing Sequence
\(x_1 \geq x_2 \geq x_3 \geq \cdots\) If a monotone deceasing sequence has an accumulation point, then the sequence must converghe to it.
Theorem 2
If $Z \subset \mathbb{R}$ is compact, then any dequence ${ x_i}_{i \in \mathbb{N}} \subset Z$ must have at least one accumulation point.
proof
Accumulation point가 아니라면 다음 그림과 같이 될 것이다.
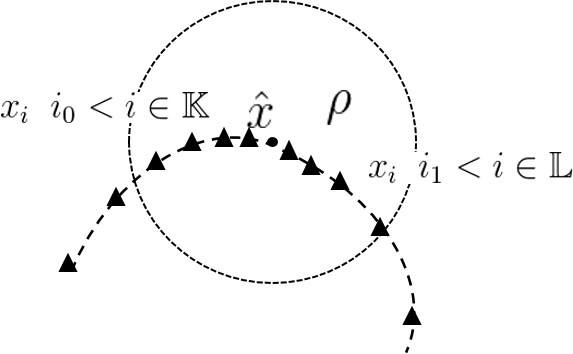
Suppose that $x_i \overset{\mathbb{K}}{\rightarrow} \hat{x}$, but $x_i \overset{\mathbb{L}}{\nrightarrow} \hat{x}$ (It means that
\[\exists \; \epsilon > 0 \;\;\text{such that}\;\; \forall i_0, \;\; \left\| x_i - \hat{x} \right\| \geq \epsilon \;\; \exists \; i \geq i_0\]i.e.
\[\exists \; \mathbb{L} \subset \mathbb{N}\;\;\text{such that}\;\; \left\| x_i - \hat{x} \right\| \geq \epsilon \;\; \forall i \in \mathbb{L}\])
Pick $i_1 \in \mathbb{K}$ satisfying that $\exists i_1 \geq i_0$ such that $\left| x_{i_1} - \hat{x} \right| < \frac{\epsilon}{4}$ (가정에서 $i \in \mathbb{K}$ 이므로 이렇게 잡을 수 있다.) Pick $i_2 \in \mathbb{L}$ satisfying that $\exists i_2 \leq i_1$ such that $\left| x_{i_2} - \hat{x} \right| \geq \epsilon$ (가정에서 $i_2 \in \mathbb{L}$ 이므로 이렇게 잡을 수 있다.)
Since $i_2 > i_1$ and $\left| x_{i_1} - \hat{x} \right| < \left| x_{i_2} - \hat{x} \right|$, it implies that $x_{i_2} \leq x_{i_1}$. (제곱을 사용하여 간단히 증명할 수 있다. 그 결과는 다음과 같다.)
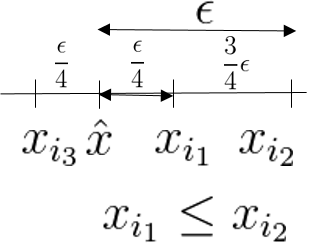
Therefore, $x_{i_1} - x_{i_2} \geq \frac{3}{4} \epsilon$ .
Pick $i_3 \in \mathbb{K}$ such that $i_3 > i_2$ then $x_{i_3} \leq x_{i_2}$, and, by assumption,
\[\left\| x_{i_3} - \hat{x} \right\| < \frac{\epsilon}{4}\]Thus,
\[\begin{align*} x_{i_2} - x_{i_3} &= x_{i_2} - x_{i_1} + x_{i_1} - x_{i_3} \\ &\leq -\frac{3}{4} \epsilon + \frac{\epsilon}{2} \\ &\leq -\frac{1}{4} \epsilon \end{align*}\]이는 가정 ($x_{i_3} \leq x_{i_2}$) 에 모순. [Q.E.D]
Continuity and Uniform Continuity
We say a function $f : \mathbb{R}^n \rightarrow \mathbb{R}^{m}$ is continuous at $x \in \mathbb{R}^n$
\[\text{If}\;\; \forall \delta > 0, \;\; \exists \varepsilon > 0 \;\;\text{such that}\;\; \left\| f(y) - f(x) \right\| < \delta \;\; \forall y \in B^o(x, \varepsilon)\](Locally Continuouis)
We say a function is uniform continuous
\[\text{If}\;\; \forall \delta > 0, \;\; \exists \varepsilon > 0 \;\;\text{such that}\;\; \forall x \in \mathbb{R}^n,\; \left\| f(y) - f(x) \right\| < \delta \;\; \forall y \in B^o(x, \varepsilon)\]($\forall x \in \mathbb{R}^n$ 조건에 의해 매우 강력한 Continuous 가 된다, 전체 영역에 대한 것이므로..)
HW 2.
$f$ is continuous at $\hat{x}$ iff for any convergent sequence ${x_i }_{i \in \mathbb{N}}$ to $\hat{x}$, $f(x_i)$ also converges to $f(\hat{x})$.
Example
$f:\mathbb{X} \rightarrow \mathcal{M}$ is continuous, and $\mathbb{X}$ is compact then $f$ is uniform continuous on $\mathbb{X}$.
Proof
Since $f$ is continuous, $\forall x \in \mathbb{X}, \;\; \forall \delta > 0, \exists \varepsilon_x > 0$ such that $\left| f(y) - f(x) \right| < \delta$ implies that $y \in B^o(x, \varepsilon_x)$. Since $\mathbb{X}$ is compact, ${B_{x \in \mathbb{X}}^o(x, \varepsilon_x) }$ covers $\mathbb{X}$ (i.e. $\bigcup_{x \in \mathbb{X}} B^o(x, \varepsilon_x) \supset \mathbb{X}$).
Moreover, Since $\mathbb{X}$ is compact, there exists a finite number of open covering, say \(\{x_i\}_{i=1}^{k}\) such that $\bigcup_{i=1}^k B^o(x_i, \varepsilon_x) \supset \mathbb{X}$. Then, pick $\varepsilon$ such that $\varepsilon = \underset{i={1 \cdots k }}{min} \varepsilon_{x_i}$.
It implies that $\varepsilon$ satisfies the property.

Lemma : Continuous on Compact Set
$\mathbb{X} \subset \mathbb{R}^n$ is compact and $f:\mathbb{R}^n \rightarrow \mathbb{R}^m$ is continuous. It implies that $f(\mathbb{X}) = { y \in \mathbb{R}^m | y = f(x), x \in \mathbb{X}} \subset \mathbb{R}^m$ is compact. (직관적으로 당연하나, 이것의 증명을 위해서는 Continuous 와 Compact의 정의를 정확히 사용하여야 한다.)
Proof
- $\mathbb{R}^n$ is compact means that it is closed and bounded.
- Proof of Closed : Limit Point가 같은 Set에 있음을 보인다. It needs to prove that for any sequence ${y_i }_{i \in \mathbb{N}} \subset f(\mathbb{Z})$ converges to $\hat{y} \in f(\mathbb{X})$.
Since ${y_i } \subset f(\mathbb{X})$ for any $y_i \in f(\mathbb{X}), \exists x_i \in \mathbb{X}$ such that $y_i = f(x_i)$. Since $\mathbb{X}$ is compact, there exists subsequence of ${x_i }_{i \in \mathbb{N}}$ such that $x_i \overset{\mathbb{K}}{\rightarrow} \hat{x}$ and $\hat{x} \in \mathbb{X}$. Since $f$ is continuous $x_i \rightarrow \hat{X}$ implies that $f(x_i) \overset{\mathbb{K}}{\rightarrow} f(\hat{x})$ … 다시말해, $\hat{x}$ is a limit point, since if it is not ${y_i}$, it cannot be a convergence sequence. then $f(x_i) \overset{\mathbb{K}}{\rightarrow} f(\hat{x}) \Leftrightarrow y_i \rightarrow \hat{y}$.
- Proof of Bounded : 제한된 값을 가짐을 보인다.
Suppose not, i.e. $\exists {y_i }_{i \in \mathbb{N}}$ such that $y_i \uparrow \infty$ as $i \rightarrow \infty$. Since $y_i \in f(\mathbb{x}), \;\; \exists x_i \in \mathbb{X}$ such that $x_i \rightarrow \hat{x} \Leftrightarrow f(x_i) \rightarrow f(\hat{x}) \Leftrightarrow y_i \rightarrow \hat{y}$, thus, $\exists i_0 \in \mathbb{N}$ such that $\left| f(x_i) \right| \leq \left| f(\hat{x}) \right| + 1 < \infty, \;\; \forall i \geq i_0$, It is contradict to assumption. Compact 가정에 어긋난다.
Derivative
Definition
\[f'(t) = \lim_{\Delta t \rightarrow 0} \frac{f(t+\Delta t) - f(t)}{\Delta t} \Rightarrow \lim_{\Delta t \rightarrow 0} \frac{f(t+\Delta t) - f(t) - f'(t) \Delta t}{\Delta t} = 0\]where $f:\mathbb{R} \rightarrow \mathbb{R}$.
Moreover, for $f:\mathbb{R}^n \rightarrow \mathbb{R}^m$, $f$ is differentiable at $x$ if $\exists Df(x)$ such that $Df(x) = J(x) \in \mathbb{R}^{m \times n}$ such that
\[\lim_{ \left\|x \right\| \rightarrow 0} \frac{\left\|f(x + \Delta x) - f(x) - D f(x) \Delta x \right\|}{\left\|x \right\|} = 0\]Example : Using Jacobian
Let $\Delta x = t \cdot e_i$ \(\lim_{ \left\|x \right\| \rightarrow 0} \frac{\left\|f(x+ t e_i) - f(x) -t \cdot J(x) e_i \right\|}{|t|} = 0\) where \(e_i = \begin{bmatrix} 0\\ 0\\ \vdots\\ 1\\ \vdots\\ 0 \end{bmatrix} \rightarrow \text{i-th Column for indexing i-th row} \;\;\text{,so that}\;\; J(x)e_i = \frac{\partial f}{\partial x_i} = \begin{bmatrix} \frac{\partial f^1}{\partial x_i}\\ \frac{\partial f^2}{\partial x_i}\\ \vdots\\ \frac{\partial f^m}{\partial x_i} \end{bmatrix} = J(x)_i\)
Taylor’s Formula
Suppose that $f:\mathbb{R}^n \rightarrow \mathbb{R}^m$ is continously differentiable (계속 미분 할 수 있다는 의미), then
\[\exists y, x \in \mathbb{R}^n, \;\; f(y) - f(x) = \int_0^1 \frac{\partial f(x+ s(y-x))}{\partial x} \cdot (y-x) ds\]Proof
Let $g(s) \triangleq f(x + s(y-x))$ such that $g(1) = y$, and $g(0)=x$. By assumption, $g(s)$ is differentiable since $f$ is continuouslu differntiable.
\[\frac{dg(s)}{ds} = \frac{df(x + s(y-x))}{dx} \cdot (y-x)\](by Chain rule, $\frac{dg(s)}{ds} = \frac{df(X(s))}{dX(s)} \cdot \frac{dX(s)}{ds}, \;\; X(s) = x + s(y-x)$, Set $X(s)$ to be $x$)
\[\begin{align*} \int_0^1 \frac{dg(s)}{ds} \cdot ds&= \int_0^1 \frac{\partial f(x+s(y-x))}{\partial x}\cdot (y-x)ds\\ \Leftrightarrow g(1) - g(0) &= \int_0^1 \frac{\partial f(x+s(y-x))}{\partial x}\cdot (y-x)ds \end{align*}\]Twice Differentiable
Let $f:\mathbb{R}^n \rightarrow \mathbb{R}$ be a twice differentiable, then, for any $x, y \in \mathbb{R}^n$
\[f(y) - f(x) = \langle \frac{\partial f(x)}{\partial x}, y-x \rangle + \int_0^1 (1-s) \langle y-x, \frac{\partial^2 f(x+s(y-x))}{\partial x^2}\cdot (y-x) \rangle ds\]proof
Let $g(s) \triangleq f(x + s(y-x))$. Then,
\[g'(s) = \frac{df(x + s(y-x))}{dx}(y-x)\](where, $\frac{df(x + s(y-x))}{dx}$ is row vector, by definition of vector differential, and $(y-x)$ is coulumn vector.) In addition,
\[g''(s) = \langle (y-x), \frac{d^2f(x + s(y-x))}{dx^2}(y-x) \rangle\]HW. $g’‘(s)$ 를 증명하라.
Then, Set
\[(1-s)g''(s) = \frac{d}{ds}\left((1-s)g'(s) + g(s) \right)\](It is a technique !!)
\[\begin{align*} \int_0^1 (1-s)g''(s) ds &= \int_0^1 \frac{d}{ds}\left((1-s)g'(s) + g(s) \right) ds \\ &= \int_0^1 d\left( (1-s)g'(s) + g(s) \right) \\ &= 0 \cdot g(s) + g(1) - g'(s) - g(0) \\ &= g(1) - g(0) - g'(s) \\ &= f(y) - f(x) - \langle \nabla f(x), y-x \rangle \end{align*}\]end of page
Comments