- Definition : Locally Lipschitz Continuous
- Definition : Globally Lipschitz Continuous
- Convexity
- Hyper Plane
Definition : Locally Lipschitz Continuous
We say $f:\mathbb{R}^n \rightarrow \mathbb{R}^m$ is Locally Lipschitz continuous at $x$, such that
\[\textit{If}\;\; \exists \rho > 0 \;\;\& \;\; L > 0 \;\;\textit{then} \;\; \forall y \in B^o(x, \rho), \\ \left\| f(x) - f(y) \right\| \leq L \cdot \left\| x - y\right\|\]- $x$ 근방의 미분치는 $L$ 보다 작다는 의미이며 꼭 미분 가능이 아니라도 성립한다.
Definition : Globally Lipschitz Continuous
\[\textit{If} \;\; \exists L > 0\;\;\textit{such that}\;\; \forall x, y \in \mathbb{R}^n \\ \left\| f(x) - f(y) \right\| \leq L \cdot \left| x - y \right\|\]Example
| Globally Lipschitz Continuous가 성립하는 경우 | Globally Lipschitz Continuous가 성립하지 않는 경우 |
|---|---|
 |
 |
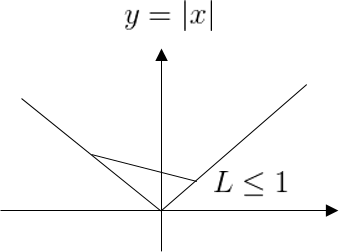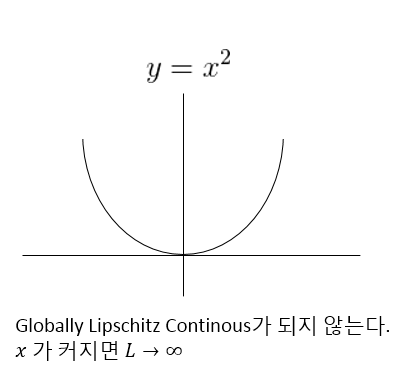Convexity
Convex Sets
We say a set $A \subset \mathbb{R}^n$ is convex, if every $x, y \in A$, the line connecting them is also in $A$. i.e. \(\forall x, y \in A, \;\; x + \lambda(y-x) \in A, \;\; \forall \lambda \in [0,1]\)
Definition : Convex Hull
Let $S \subset \mathbb{R}^n$, A convex hull, $coS$, is the smallest convex set containing the set $S$.
Theorem C-1
Let $S \subset \mathbb{R}^n$ . If $\bar{x} \in coS$ then there exist at most $n+1$ distinct points \(\{x_i\}_{i=1}^{n+1}\) in $S$ such that $\bar{x}=\sum_{i=1}^{n+1} \mu^i x_i, \;\; \mu^i > 0, \;\sum_{i=1}^{n+1}\mu^i = 1$
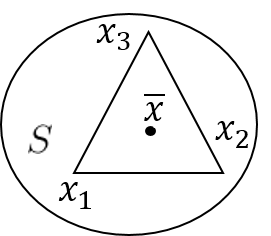두 점으로는 이렇게 만들기 어렵다는 것을 의미한다. 즉, 볼록 다항식이 Convex Set 안에 정의될 수 있음을 의미한다.
Definition C-1
Consider a set
\[C_s = \{ x \in \mathbb{R}^n | x=\sum_{i=1}^{k_x} \mu_i x_i, \;\; x_i \in S, \;\; \mu_i \geq 0, \;\; k_x \in \mathbb{N}, \;\; \sum_{i=1}^{k_x} \mu_i = 1\}\]Lemma C-1
$C_s = coS$
Proof of Lemma
- $C_s \supset coS$
- $C_s \subset coS$ 1, 2를 증명해야 한다.
proof of $C_s \supset coS$
For any $x’, x’’ \in S$, and $\bar{x} \in coS$ such that
\[x' + \lambda(x'' - x') = (1-\lambda)x' + \lambda x'' \in C_s \;\; \forall \lambda \in [0,1]\](i.e. $\bar{x} = x’ + \lambda(x’’ - x’)$ Since $\mu_1 = 1 - \lambda \geq 0$, $\mu_2 = \lambda \geq 0$, then $\mu_1 + \mu_2 = 1$. It implies that $C_s \supset coS$ (Since $S \subset coS$) by definitionof $C_s$.
이를 통해 $C_s$가 Convex임이 증명되며 동시에 $coS$는 $S$의 smallest convex 이므로 $C_s \supset coS$ 이다.
proof of $C_s \subset coS$
Pick any $ x \in C_s$, i.e. $ x = \sum_{i=1}^{k_x} \mu^i x_i $. Since $x_i \in S \subset coS$ and
\(\begin{align*} x &= \mu^{k_x} x_k + \sum_{i=1}^{k_x - 1} \mu^i x_i = (1 - \sum_{i=1}^{k_x - 1} \mu^i) x_k + \sum_{i=1}^{k_x - 1} \mu^i x_i \\ &= \sum_{i=1}^{k_x - 1} \left( (1 - \mu^i)x_k + \mu^i x_i \right) - (k_x - 2) x_k \end{align*}\) Set $x_k^c \in coS$ such that $x_k^c = (1 - \mu^i)x_k + \mu_i x_i$ \(x = \sum_{i=1}^{k_x - 1} x_k^c - (k_x -2)x_k\)
Let new parameter $\bar{\mu}^i$ for $x_k^c$ to be 1 for all $i \leq kx -1$ and $\bar{\mu}^{k_x} = -k_x + 2$. Since the sum of the new parameter $\bar{\mu}^i$ is $\sum_{i=1}^{k_x} \mu^i = k_x - 1 - k_x + 2 = 1$, the $x$ is still in $C_s$ and also in $coS$. Thus, $C_s \subset coS$.
Q.E.D of Lemma
Proof of Theorem
Since $\bar{x} \in coS = C_s$, $\exists k$ and $\mu_i$ such that $\bar{x} = \sum_{i=1}^k \mu^i x_i$, where $x_i \in S$, $\mu^i \geq 0$, and $\sum_{i=1}^k \mu^i = 1$. Set the above condition as to be
\[\sum_{i=1}^k \mu^i \begin{bmatrix} x_i \\ 1 \end{bmatrix} = \begin{bmatrix} \bar{x} \\ 1 \end{bmatrix} \tag{1}\]Since ${ x_i}1^k \subset \mathbb{R}^n $ and $k > n+1$, ${ x_i}_1^k$ are linear dependent. Since the vector made by the sequence is linear dependent, there exist ${ \alpha_i}{i=1}^k$ such that
\[\sum_{i=1}^k \alpha^i \begin{bmatrix} x_i \\ 1 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} \tag{2}\](1) + (2) $\times \theta$ for some $\theta$, we can obtain
\[\sum_{i=1}^k (\mu^i + \theta \alpha^i ) \begin{bmatrix} x_i \\ 1 \end{bmatrix} = \begin{bmatrix} \bar{x} \\ i \end{bmatrix}\]Since there is $i$ such that $\alpha^i < 0$, there exists $\bar{\theta} > 0$ such that $\mu^i + \bar{\theta} \alpha^i = 0$, and $\mu^j + \bar{\theta} \alpha^j > 0. \; i \ne j$ 결국 $\bar{\theta}$를 잘 선택하면 하나의 component가 사라진다. 그래도 위 방정식은 성립한다.
We have at most $k-1$ nonzero $\mu^j + \bar{\theta} \alpha^j$ and $\sum_j (\mu^j + \bar{\theta}\mu^j) = 1$ and $\sum_j (\mu^j + \bar{\theta}\mu^j) > 0$. Keep doing this intil $k=n+1$.
Q.E.D of Theorem
Hyper Plane
Definition : Hyper Plane
$S_1, S_2$ be any sets in $\mathbb{R}^n$, we say that the ** Hyper Plane **
\[H = \{ x \in \mathbb{R}^n | \langle x, v\rangle = \alpha \}.\]where $\alpha \in \mathbb{R}, \;\; v \in \mathbb{R}^n$ are given. Separate $S_1$ and $S_2$, if
\[\begin{align} \langle x, v \rangle &\geq \alpha, \;\; \forall x \in S_1\\ \langle x, v \rangle &\leq \alpha, \;\; \forall x \in S_2 \end{align}\]
Theorem H-1
Let $S_1$ and $S_2$ be ** compact and convex sets ** in $\mathbb{R}^n$. Suppose that $S_1 \cap S_2 = \emptyset$, then there exists a hyper plane which seperate $S_1$ and $S_2$.
Lemma H-1
Let $S$ be a compact and convex subset of $\mathbb{R}^n$. Suppose that $O \notin S$. Let $\hat{x} = \arg \min {||x|| | x \in S }$, then $\forall x \in S, \langle x - \hat{x}, \hat{x} \rangle \geq 0$.
Proof of Lemma H-1
\[x(\lambda) = \hat{x} + \lambda(x - \hat{x}) \;\; \lambda \in [0,1], \; \textit{and}\; x \in S\]Since $\hat{x} = \arg \min {||x|| | x \in S }$, $\forall \lambda \in [0,1], \;\; \left| x(\lambda) \right|^2 \geq \left| \hat{x} \right|^2$. Accordingly,
\[\langle \hat{x} + \lambda (x - \hat{x}), \hat{x} + \lambda (x - \hat{x}) \rangle = \left\| \hat{x} \right\|^2 + 2 \lambda \langle x - \hat{x}, \hat{x} \rangle + \lambda^2 \left\| x - \hat{x} \right\| \geq \left\| \hat{x} \right\|^2 \\ \Leftrightarrow 2 \lambda \langle x - \hat{x}, \hat{x} \rangle + \lambda^2 \left\| x - \hat{x} \right\| \geq 0 \\ \Leftrightarrow \langle x - \hat{x}, \hat{x} \rangle \geq \frac{1}{2} \lambda \left\| x - \hat{x} \right\|\]Let $\lambda \rightarrow 0$, then $\langle x - \hat{x}, \hat{x} \rangle \geq 0$ Q.E.D pf Lemma H-1
Proof of Thorem H-1
Let
\[C = S_1 - S_2 \triangleq \{ x \in \mathbb{R}^n | x = x_1 - x_2, \; x_1 \in S_1, x_2 \in S_2\}\]Since $S_1 \cap S_2 = \emptyset$ and ** $C$ is convex and comapct ** (But it is not proven.!!)
Lemma H-2
$C$ is convex
Proof of Lemma H-2
다음을 증명하는 것이다.
\[\forall y_1, y_2 \in C \Rightarrow \lambda y_1 + (1-\lambda)y_2 \in C\]따라서 다음과 같이 $x_{11} \in S_1,\;\; x_{12} \in S_2$를 가정하자.
\[\begin{align} y_1 \in C &\Rightarrow \exists x_{11} \in S_1, \;\ x_{12} \in S_2 \;\; \textit{such that} \;\; x_{11} - x_{12} = y_1 \\ y_2 \in C &\Rightarrow \exists x_{21} \in S_1, \;\ x_{22} \in S_2 \;\; \textit{such that} \;\; x_{21} - x_{22} = y_2 \end{align}\]The above equation implies that
\[\begin{align} \lambda y_1 + (1-\lambda) y_2 &= \lambda (x_{11} - x_{12}) + (1 - \lambda )(x_{21} - x{22}) \\ &= \lambda x_{11} + (1 - \lambda )x_{21} - \left( \lambda x_{12} + (1 - \lambda)x_{22}\right) \in C \end{align}\]Since
\[\begin{align} \lambda x_{11} + (1 - \lambda )x_{21} \in S_1 \\ \lambda x_{12} + (1 - \lambda )x_{22} \in S_2 \end{align}\]Hence, $C$ is convex. Q.E.D. of Lemma H-2
Lemma H-3
$C$ is compact
Proof of Lemma H-3
Bound
(It is obvious. 다음을 증명하는 것이다.) $\exists M < \infty$ such that $\forall y \in C$, $\left| y \right| \leq M$.
Since $S_1, S_2$ is compact $\exists M_1, M_2 < \infty$ such that $\left| x_1 \right| \leq M_1, \forall x_1 \in S_1$ and $\left| x_2 \right| \leq M_2, \forall x_2 \in S_2$.
$y \in C$ implies that $\exists x_1 \in S_1, x_2 \in S_2$ such that $y = x_1 - x_2$ Thus,
\[\left\| y \right\| \leq \left\| x_1 \right\| + \left\| x_2 \right \| \leq M_1 + M_2\]Closed
Pick any convergent sequence ${ y_i }_{i=1}^{\infty} \subset C, \; y_i \rightarrow \bar{y}$ 이어서 $\bar{y} \in C$ 임을 증면하는 것이다.
Since $S_1, S_2$ is compact,
\[\exists \{x_{i_1} \}_{i_1=1}^{\infty} \subset S_1, \; \{x_{i_2} \}_{i_2=1}^{\infty} \subset S_2\]Since $y_i = x_{i_1} - x_{i_2}$ and $x_{i_1} \rightarrow \bar{x_1}$ and $x_{i_2} \rightarrow \bar{x_2}$, there exists $\bar{y} \in C$. Q.E.D. of Lemma H-3
Continue to proof of Theorem H-1
Let \(\hat{z} = \arg \min \left\{ \left \| z \right \| | z \in C \right\}\) where $\hat{z} = \frac{1}{2} (x_2 - x_1)$ for $x_1, x_2$ is satisfying $\arg \min {x_1, x_2 | \left| x_1 - x_2 \right| }$
from the Lemma H-1
\[\langle x_1 - \hat{z}, \hat{z} \rangle = \langle x_1, \hat{z} \rangle - \left\| \hat{z} \right\|^2 \geq 0 \Rightarrow \langle x_1, \hat{z} \rangle \geq \left\| \hat{z} \right\|^2 \tag{3}\]$\hat{z}$의 정의에 의해 (and $O \notin C$)
\[\langle \hat{z} - x_2, \hat{z} \rangle = \left\| \hat{z} \right\|^2 - \langle x_2, \hat{z} \rangle \geq 0 \Rightarrow \langle x_2, \hat{z} \rangle \leq \left\| \hat{z} \right\|^2\]Q.E.D. of Theorem H-1
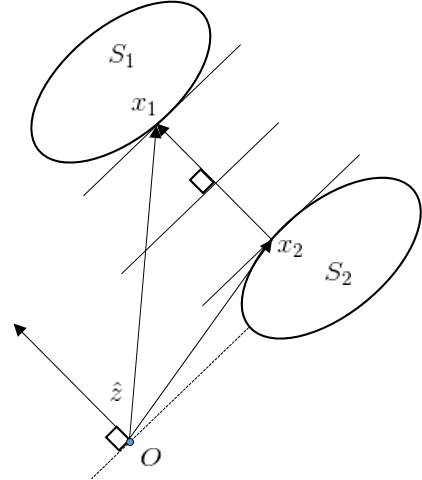
Comments