Convex Function
Definition : Convex function
$f:\mathbb{R}^n \rightarrow \mathbb{R}$ is said to be convex. If $\forall x, y \in \mathbb{R}^n, \;\; \lambda \in [0,1]$, then
\[f(x + \lambda(y-x)) \leq (1-\lambda) f(x) + \lambda f(y)\]
Example
Lyapunov Function $x^T P x$
- 모든 convex function은 Global minima를 쉽게 찾을 수 있다.
Definition : Epi-Graph
\[E_{pi}(f) \triangleq = \left\{ \begin{bmatrix} x^o \\ x \end{bmatrix} \in \mathbb{R}^{n+1} | x^o \geq f(x) \right\}\]Example
Epi-Graph of $f:\mathbb{R} \rightarrow \mathbb{R}$, $f(x) = x^2$.
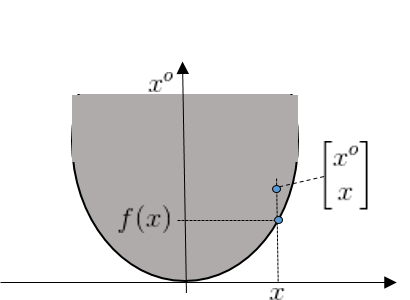
Lemma C-1
Suppose $f:\mathbb{R}^n \rightarrow \mathbb{R}$ is convex, then Epi($f$) is a convex set
Proof is omitted (or HW)
Definition : Simplex
Simplex $[a_1, \cdots, a_{n+1}]$ : $a_1 \cdots a_n$ 이 꼭지점이 되어 이루어진 도형과 그 내부 It implies that $a \in \textit{int}(A)$, where $\textit{int}(A)$ is interior point of $A$, and $\textit{int}(A)$ is an open set.

Theorem C-1
Let $G$ be a convex set in $\mathbb{R}^n$, If $f : G \rightarrow \mathbb{R}$ is a convex, then $f$ is continuous in $G$.
proof of Theorem C-1
Let $a \in G$, By Caratheodory theorem,
\(\exists (n+1) \;\textit{simplex} [a_1, \cdots, a_{n+1}], a_i \in G, \;\; \textit{such that} \;\; a \in \textit{int}(A)\) where $A$ is simplex. It implies that $\exists \delta > 0$ such that $a \in B^o(a, \delta) \subset \textit{int}(A)$ ( Obviously!!) then $\forall x \in A$, $f(x) \leq \alpha$ . (그림 참조)
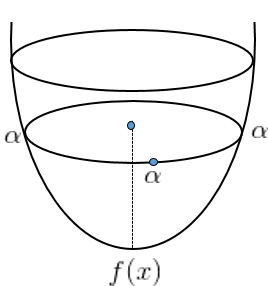
Since $A \subset G$, and $G$ is convex, $\exists \mu_i$ for $i=1, \cdots n+1$, such that $\sum_{i=1}^{n+1}\mu_i \alpha_i = x$, $\mu_i \geq 0$, $\sum_{i=1}^{n+1} \mu_i = 1$. Thus,
\[f(x) = f(\sum_{i=1}^{n+1}\mu_i \alpha_i) \leq \sum_{i=1}^{n+1} \mu_i f(\alpha_i) \leq \alpha \sum_{i=1}^{n+1}\mu_i \tag{1}\](Obviolusly, Convex 이므로)
Pick any $x_o \in B^o(a, \delta)$. Let $z = x - x_0$, then $f_z(z) = f(x) - f(x_0)$ Since $B^o(a, \delta)$ is open, $\exists \lambda > 0$ such that $B(x^o, \lambda) \subset B(a, \delta)$ (Open set 이므로 이러한 Open Set 은 당연히 존재한다.)
이 상태에서 다음을 증명해야 한다. (Continuous의 정의에 따라)
\[\textit{For any}\;\; \varepsilon > 0, \;\; \exists \rho > 0 \;\;\textit{such that}\;\;\left\| z \right\| < \rho \Rightarrow \left\| f_z(z) \right\| \leq \varepsilon\]for any $\varepsilon > 0$, pick $z$ such that $\left| \frac{z}{\varepsilon} \right| < \lambda \Rightarrow \left| z \right| < \varepsilon \lambda$ ($\rho = \varepsilon \lambda$)
\[f_z(z)=f_z\left( (1-\varepsilon) \cdot 0 + \varepsilon \frac{z}{\varepsilon} \right) \leq (1-\varepsilon) f_z(0) + \varepsilon f_z(\frac{z}{\varepsilon}) = \varepsilon f_z(\frac{z}{\varepsilon}) \leq 2 \alpha \varepsilon \tag{2}\](Since $f(x) \leq \alpha$, $f_z(z) = f(x) - f(x_0) \leq \left| f(x) \right| + \left| f(x_0) \right| \leq 2\alpha$ )
In addition,
\[0 = f_z(0) = f_z \left( \frac{1}{1 + \varepsilon} z + \frac{\varepsilon}{1+\varepsilon} \cdot - \frac{z}{\varepsilon} \right) \leq \frac{1}{1+\varepsilon}f_z(z) + \frac{\varepsilon}{1+\varepsilon}f_z(-\frac{z}{\varepsilon}) \tag{3}\](Equation (1) 에서 당연)
방정식 (3)의 우측항은 결국
\[0 \leq \frac{1}{1+\varepsilon}f_z(z) + \frac{\varepsilon}{1+\varepsilon}f_z(-\frac{z}{\varepsilon}) \Rightarrow -\varepsilon f_z(-\frac{z}{\varepsilon}) \leq f_z(z)\]이므로
\[-2\alpha \varepsilon \leq -\varepsilon f_z(-\frac{z}{\varepsilon}) \leq f_z(z) \tag{4}\]방정식 (2), (4)에서
\[-2\alpha \varepsilon \leq f_z(z) \leq 2\alpha \varepsilon \Rightarrow |f_z(z)| \leq 2\alpha \varepsilon\]Q.E.D of THeorem C-1
Theorem C-2
$f$ is differentiable then $f$ is **convex iff ** $\forall x, y \in \mathbb{R}^n$
\[f(y) - f(x) \geq \langle \nabla f(x), (y-x) \rangle\]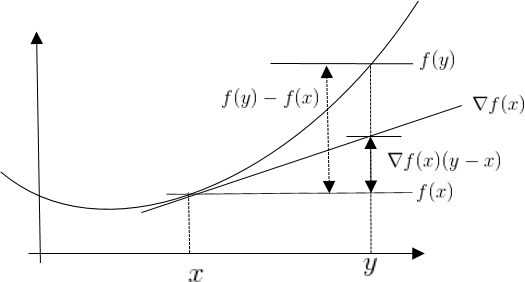
Remind : Differentiable
\[f(y) - f(x) = \int_0^1 \frac{\partial f(x+s(y-x))}{\partial x} (y-x) ds\]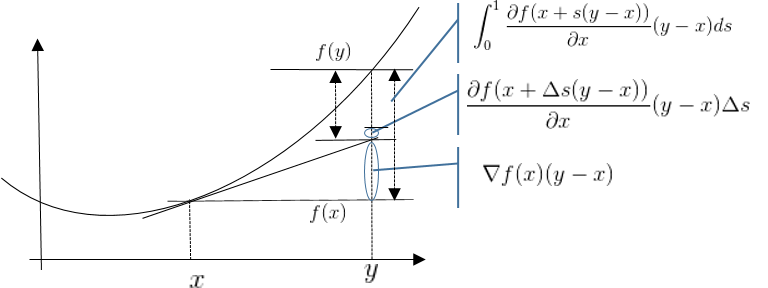
Proof of theorem C-2
Proof of Necessity ($\Rightarrow$)
Since $f$ is convex i.e.
\[f(\lambda x + (1-\lambda)y) \leq \lambda f(x) + (1-\lambda) f(y)\]and $f$ is differentiable i.e.
\[f(y) - f(x) = \int_0^1 \langle \nabla f(x + s(y-x)), y-x \rangle ds\]그러므로 x, y 사이의 한 점 $\lambda x + (1-\lambda) y, \;\; \forall \lambda \in [0,1]$ 에 대하여
\[\begin{align} f(\lambda x + (1-\lambda) y) - f(x) &= \int_0^1 \langle \nabla f(x + s(\lambda x + (1-\lambda) y - x))), (1-\lambda)(y-x) \rangle ds \\ &= \int_0^1 \langle \nabla f(x + s(1-\lambda)(y - x)), (1-\lambda)(y-x) \rangle ds \\ &= (1-\lambda)\int_0^1 \langle \nabla f(x + s(1-\lambda)(y - x)), (y-x) \rangle ds \end{align}\]따라서 Convex 조건에서
\[f(\lambda x + (1-\lambda) y) = f(x) + (1-\lambda)\int_0^1 \langle \nabla f(x + s(1-\lambda)(y - x)), (y-x) \rangle ds \leq \lambda f(x) + (1-\lambda) f(y)\]it implies that
\[(1-\lambda)\int_0^1 \langle \nabla f(x + s(1-\lambda)(y - x)), (y-x) \rangle ds \leq (1-\lambda) (f(y) - f(x)) \\ \Rightarrow \int_0^1 \langle \nabla f(x + s(1-\lambda)(y - x)), (y-x) \rangle ds \leq f(y) - f(x)\]Let $\lambda \rightarrow 1$, then
\[\int_0^1 \langle \nabla f(x), (y-x) \rangle ds \leq f(y) - f(x) \Rightarrow \langle \nabla f(x), (y-x) \rangle \int_0^1 ds \leq f(y) - f(x)\]Q.E.D of Necessity
Proof of Suffciency ($\Leftarrow$)
\[f(y) - f(x + \lambda(y-x)) \geq \langle \nabla f(x + \lambda(y-x)), (1-\lambda)(y-x) \rangle \tag{1}\] \[f(x) - f(x + \lambda(y-x)) \geq \langle \nabla f(x + \lambda(y-x)), -\lambda(y-x) \rangle \tag{2}\](식 (2)의 경우 방향이 반대이므로 $\lambda$에 마이너스가 붙었다.)
(1) $\times \lambda +$ (2)$\times (1-\lambda)$
\[\lambda f(y) + (1 - \lambda) f(x) - \lambda f(x + \lambda(y-x)) - (1 - \lambda) f(x + \lambda(y-x)) \geq 0 \\ \Rightarrow \lambda f(y) + (1 - \lambda) f(x) \geq f(x + \lambda(y-x))\]Convex 증명, 자동적으로 continuous 증명 그러므로 Differentiable 까지 증명 Q.E.D of Sufficiency
Theorem C-3
$f$ is twice continuosly differentiable, then $f$ is convex iff
\[\frac{\partial^2 f(x)}{\partial x^2} \geq 0, \forall x \in \mathbb{R}^n\]Definition : Semipositive definite
$f:\mathbb{R}^n \rightarrow \mathbb{R}$ 에 대하여 \(\frac{\partial^2 f(x)}{\partial x^2} \geq 0, \forall x \in \mathbb{R}^n\) 이면 Semipositive definite이라 하며, 이는 $\forall x \in \mathbb{R}^n$ 에 대하여 \(\langle x, \frac{\partial^2 f(x)}{\partial x^2} x \rangle \geq 0\) 을 의미한다.
Proof of theorem C-2
Proof of Necessity ($\Rightarrow$)
Since $f:\mathbb{R}^n \rightarrow \mathbb{R}$ is twice differentiable i.e.
\[f(y) -f(x) = \langle \nabla f(x), y-x \rangle + \int_0^1 (1-s)\langle y-x, \frac{\partial^2 f}{\partial x^2}(x+s(y-x)) \left( y-x\right) \rangle ds\]By Theorem C-2,
\[0 \leq f(y) - f(x) - \langle \nabla f(x), y-x \rangle\]Hence,
\[\frac{f(y) - f(x) - \langle \nabla f(x), y-x \rangle}{\left\| y-x \right\|^2} \geq 0\]Accordingly,
\[\frac{f(y) - f(x) - \langle \nabla f(x), y-x \rangle}{\left\| y-x \right\|^2} = \int_0^1 (1-s) \langle \frac{y-x}{\left\| y-x \right\|}, \frac{1}{\left\| y-x \right\|} \langle y-x, \frac{\partial^2 f}{\partial x^2}(x+s(y-x)) \left( y-x\right) \rangle ds \geq 0\]Let $ y \rightarrow x$, then $\frac{y-x}{\left| y-x \right|} = z$ is a normal vector. Therefore,
\[\langle z, \frac{\partial^2 f(x)}{\partial x^2} z \rangle \int_0^1 (1-s) ds \geq 0 \;\;\Leftrightarrow \;\; \frac{1}{2} \langle z, \frac{\partial^2 f(x)}{\partial x^2} z \rangle \geq 0\]Consequently, $\frac{\partial^2 f(x)}{\partial x^2}$ is Positive SemiDefinite. Q.E.D of Necessity
Proof of Sufficiency ($\Leftarrow$)
Rewrite the twice differential as
\[f(y) -f(x) - \langle \nabla f(x), y-x \rangle = \int_0^1 (1-s)\langle y-x, \frac{\partial^2 f}{\partial x^2}(x+s(y-x)) \left( y-x\right) \rangle ds\]By Assunption, $\frac{\partial^2 f}{\partial x^2}(x+s(y-x)) \geq 0\;\; \forall \lambda \in [0,1]$. Thus,
\[0 \leq \int_0^1 (1-s)\langle y-x, \frac{\partial^2 f}{\partial x^2}(x+s(y-x)) \left( y-x\right) \rangle ds = f(y) -f(x) - \langle \nabla f(x), y-x \rangle\]It implis that
\[f(y) -f(x) \geq \langle \nabla f(x), y-x \rangle\]By Theorem C-2, If the above condifition is satisfied, then the function $f$ is convex. Q.E.D of Sufficiency
Comments