- Form
- Definition : Level set
- Definition : Tangent Set
- Definition : Normal Set
- Theorem U-1 : Mean Value Theorem
- Directional Derivative
Form
\[\min_{x \in \mathbb{R}^n} f(x), \;\; \textit{for}\;\; f: \mathbb{R}^n \rightarrow \mathbb{R}\]where $f$ is continuosly differentiable.
Definition : Level set
Let $f: \mathbb{R}^n \rightarrow \mathbb{R}$. For given $\alpha \in \mathbb{R}$, we say the set $L_{\alpha} \subset \mathbb{R}^n$ defined by
\[L_{\alpha} = \{ x \in \mathbb{R}^n | f(x) \leq \alpha \}\]is called “a level set of $f$”
Properties
- If $\alpha_1 > \alpha_2$ then $L_{\alpha_1} \supset L_{\alpha_2}$
- If $\hat{\alpha} = \min f(x)$, then $L_{\hat{\alpha}}$ is the solution set
- An algorithm solving $\min f(x)$ is called a descent method.
If the seq ${ x_i}_{i=1}^{\infty}$ generated by algorithm, satisfy that
\[f(x_{i+1}) < f(x_i)\;\; \forall i \in \mathbb{N}\]Definition : Tangent Set
The level set of tangent to the boundary of $L_{\alpha}$, i.e. $\partial L_{\alpha}$, at a point $\hat{x} \in \partial L_{\alpha}$ is defined by.
\[T(\hat{x}, \partial L_{\alpha}) \triangleq \{ y \in \mathbb{R}^n | \beta y = \lim \frac{x_i - \hat{x}}{\left\| x_i - \hat{x} \right\|}, \;\; \overset{\beta > 0}{x_i \in}\partial L_{\alpha}\;\; \forall i \}\]아래 그림과 같은 불연속의 경우 $T(\hat{x}, \partial L_{\alpha})$는 아래 위로 두 원소를 가진다.

Definition : Normal Set
The set of normals to the boundary of $L_{\alpha}$ at a point $\hat{x} \in \partial L_{\alpha}$ is defined by
\[N(\hat{x}, \partial L_{\alpha}) \triangleq \{ \nu \in \mathbb{R}^n | \langle \nu, y \rangle = 0, \;\; y \in T(\hat{x}, \partial L_{\alpha})\}\]We say that $\nu$ is an outward normal at $\hat{x} \in \partial L_{\alpha}$ If $f(\hat{x} + \lambda \nu) > f(\hat{x})$ for sufficiently small $\lambda > 0$.
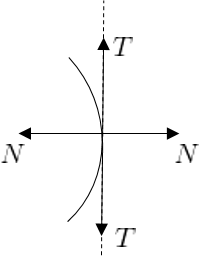
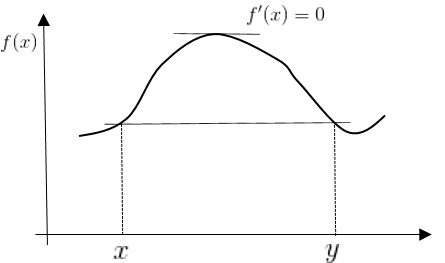
Theorem U-1 : Mean Value Theorem
For $f \in \mathbb{C}’, \;\; f:\mathbb{R}^n \rightarrow \mathbb{R}$
\[f(x)=f(y), \;\; \exists s \in [0,1]\;\;\textit{such that}\;\; f(y)-f(x) = \langle \nabla f(x + s(y-x)), y-x \rangle\]($f(x)=f(y)$ 일 경우는 밑의 그림과 같다.)
Property U-1
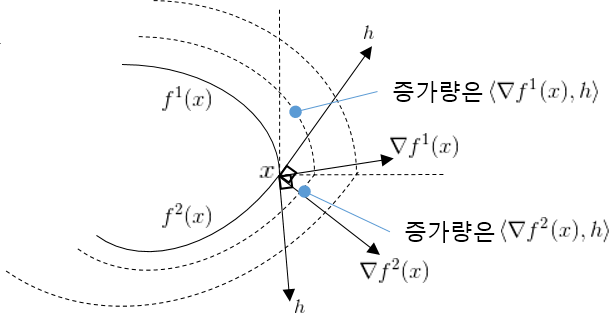
Suppse that $x \in \mathbb{R}^n$ such that $f(x) = \alpha$ If a vector $\nabla f(x) \neq 0$, then $\nabla f(x)$ is outward normal to the boundary $\partial L_{\alpha}$ at $x$.
증명을 위해 필요한 부분
- $\nabla f(x) \in \mathbb{N}(x, \partial L_{\alpha})$
- $f(x + \lambda \nabla f(x)) > f(x)$ for some sufficient small $\lambda \geq 0$
Proof of Property U-1
Proof of 1
Pick any sequence ${ \Delta x_i }{i=1}^{\infty} $ such that $x + \Delta x_i \in \partial L{\alpha}$ and $\Delta x_i \rightarrow 0, \;\; \forall i \in \mathbb{N}$ (i.e. $f(x+\Delta x_i) = \alpha$ ) <- 수식을 해석해 보면 딱 이 의미임.
For each $i \in \mathbb{N}$ by Mean-Value Theorem,
\[\exists s_i \in [0,1] \;\; \textit{such that}\;\; f(x+\Delta x_i) = f(x) + \langle \nabla f(x+s_i \Delta x_i), \Delta x_i \rangle\]implies that
\[\langle \nabla f(x+s_i \Delta x_i), \Delta x_i \rangle = 0, \;\; i \in \mathbb{N} \Rightarrow \langle \nabla f(x+s_i \Delta x_i), \frac{\Delta x_i}{\left\| \Delta x_i \right\|} \rangle = 0\]Let $y_i = \frac{\Delta x_i}{\left| \Delta x_i \right|}$, then $\exists y$ such that $y_i \rightarrow y$. (It means that $\left| y_i \right| = 1 \Rightarrow B^o(0,1)$: Closed and Bounded. Compact!!)
\[\begin{align} 0 &= \lim_{i \rightarrow \infty} \langle \nabla f(x + s_i \Delta x_i), \frac{\Delta x_i}{\left\| \Delta x_i \right\|} \rangle \\ &= \langle \nabla f(x + s_i \Delta x_i), \lim_{i \rightarrow \infty} \frac{\Delta x_i}{\left\| \Delta x_i \right\|} \rangle \\ &= \langle \nabla f(x + s_i \Delta x_i), \lim_{i \rightarrow \infty} y_i \rangle \\ &= \langle \nabla f(x + s_i \Delta x_i), y \rangle \\ \end{align}\]By the definition of $T(x, \partial L_{\alpha})$
\[y \in T(x, \partial L_{\alpha})\]Therefore, $\nabla f(x) \in \mathbb{N}(x, \partial L_{\alpha})$ (Tangent Space에 있는 $y$와 Inner Product 값이 0 이므로)
Proof of 2
By Mean Value Theorem
\[\forall \lambda > 0, \;\; \exists S_{\lambda} \in [0,1] \;\;\textit{such that} \;\; f(x+\lambda \nabla f(x)) = f(x) + \langle \nabla f(x + s_{\lambda} \lambda \nabla f(x), \lambda \nabla f(x) \rangle)\]($x + \lambda \nabla f(x) - x = \lambda \nabla f(x)$ … 두번쨰 항의 $\langle , \rangle$ 내부가 이렇게 된 이유.)
Object : $f(x + \lambda \nabla f(x)) - f(x) > 0$ for sufficiently small $\lambda > 0$ implies that $\lambda \langle \nabla f(x + s_{\lambda} \lambda f(x)), \nabla f(x) \rangle > 0$ for sufficiently small $\lambda > 0$.
By Continuity of $\nabla f(x)$ at $x$, (즉, 어떤 $\left| x \right| < \delta$ 존재하여 $\left| \nabla f(x) \right| < \varepsilon \;\; \forall \varepsilon > 0$)
\[\exists \bar{\lambda} \;\;\textit{such that}\;\; 0 < \lambda \leq \bar{\lambda} \;\;\textit{such that}\;\; \langle \nabla f(x+s_{\lambda} \bar{\lambda} \nabla f(x)), \nabla f(x) \rangle \geq \frac{1}{2} \left\| \nabla f(x) \right\|\]따라서, $\nabla f(x)$ is an outward normal.
Q.E.D. of Property U-1
Corollary U-1 : descent direction
If $x \in \mathbb{R}^n$ is such that $\nabla f(x) \neq 0$, then any vector $h \in \mathbb{R}^n$ such that $\langle \nabla f(x), h \rangle < 0$ is a descent direction for $f(\cdot)$ at $x$. i.e.
\[\exists \hat{\lambda} > 0 \;\;\textit{such that}\;\; f(x+\hat{\lambda} h) - f(x) < 0\]Note
**Differentiable Convex ** 의 정의에 따르면
\[f(y) - f(x) \geq \langle \nabla f(x), (y-x) \rangle\]이다. 그러므로 $y=x+\hat{\lambda} h$ 인데, $\left| y \right| > \left| x \right|$ 이라면, 오히려 $f(x+\hat{\lambda} h) - f(x) > 0$ 이어야 한다. 이는 이미 Property U-1에서 증명된 것이다. 따라서 이것이 반대가 되기 위해서는 $\left| y \right| \leq \left| x \right|$ 이어야 한다, 그 경우 $\langle \nabla f(x+s_{\lambda} \hat{\lambda} \nabla f(x)), \nabla f(x) \rangle \geq \frac{1}{2} \left| \nabla f(x) \right|$ 이지만, $\left| y \right| \leq \left| x \right|$ 이므로 부호가 바뀌어서
\[f(x+\hat{\lambda} h) - f(x) = \hat{\lambda} \langle \nabla f(x+s_{\lambda} \bar{\lambda} \nabla f(x)), \nabla f(x) \rangle \leq -\hat{\lambda}\frac{1}{2} \left\| \nabla f(x) \right\|\]가 된다.
증명은 생략한다.
Directional Derivative
Directional Derivative at $x$ along the vector $h$ is defined by
\[df(x,h) = \lim_{\lambda \downarrow 0} \frac{f(x+\lambda h) - f(x)}{\lambda}\]where $\lambda \downarrow 0$ means that $\lambda$ is Monotone decreasing on $\mathbb{R}^+$, and $\lambda \uparrow 0$ is Monotone increasing on $\mathbb{R}^-$.
- If $f$ is continuosly differentiable, then
imnplies that
\[\frac{f(x+\lambda h) - f(x)}{\lambda} = \int_0^1 \langle \nabla f(x + s \lambda h), h \rangle ds\]Let $\lambda \downarrow 0$, then
\[\begin{align} df(x, h) &= \lim_{\lambda \downarrow 0} \frac{f(x+\lambda h) - f(x)}{\lambda} \\ &= \lim_{\lambda \downarrow 0} \int_0^1 \langle \nabla f(x + s \lambda h), h \rangle ds \\ &= \int_0^1 \langle \lim_{\lambda \downarrow 0} \nabla f(x + s \lambda h), h \rangle ds \\ &= \langle \nabla f(x ), h \rangle \int_0^1 ds \\ &= \langle \nabla f(x ), h \rangle \end{align}\]즉
\[df(x,h) = \langle \nabla f(x ), h \rangle\]Note
많은 경우 $x$를 생략하고 $df(h)$ 를 많이 사용한다. 여기서는 최적화 알고리즘 도출을 위해서 $x$를 굳이 표시하였다. 그 외에 $h[f] = h(f)$ 역시 같은 의미로 사용한다. (미분 기하학, 리만 기하학, 미분 다양체론 등에서..)
Comments