- Definition T-1 : Relative or Local Minima
- Definition T-2 : Global Minima
- Definition T-3
- First Order Necessary Condition
Definition T-1 : Relative or Local Minima
A point $x^* \in \Omega$ is said to be a relative minimum point (or local minimum point) of $f$ over $\Omega$, if $\exists \varepsilon > 0$ such that
\[f(x) \geq f(x^*) \;\; \forall x \in B^o(x^*, \varepsilon) \cap \Omega\]and if $f(x) \geq f(x^), \;\; \forall x \in B^o(x^, \varepsilon) \cap \Omega, \;\; x \neq x^$, then $x^$ is called Strictly Relative or Local minumum point

Definition T-2 : Global Minima
A point $x^* \in \Omega$ is said to be **Global minimum point of $f$ over $\Omega$, If
\[f(x) \geq f(x^*) \;\; \forall x \in \Omega\]and if
\[f(x) \geq f(x^*) \;\; \forall x \in \Omega \;\; x \neq x^*\]then $x^*$ is Strictly global minimum point of $f$.
Definition T-3
Given a vector $x \in \Omega$ , we say a vector $h$ a feasible direction of $x$
\[\textit{If}\;\; \exists \bar{\lambda} > 0 \;\; \textit{such that} \;\; x+\lambda h \in \Omega \;\; \forall \lambda \in [0, \bar{\lambda}]\]First Order Necessary Condition
Theorem F-1 : First Order Necessary Condition
Let $\Omega \supset \mathbb{R}^n, \;\; \textit{and} \;\; f \in \mathbb{C}^1, \Omega \Rightarrow \mathbb{R} $. If $x^$ is a local minimum point of $f$ over $\Omega$, then $\forall d \in \mathbb{R}^n$ that is a feasible direction at $x^$, we have
\[\langle \nabla f(x^*), d \rangle \geq 0\]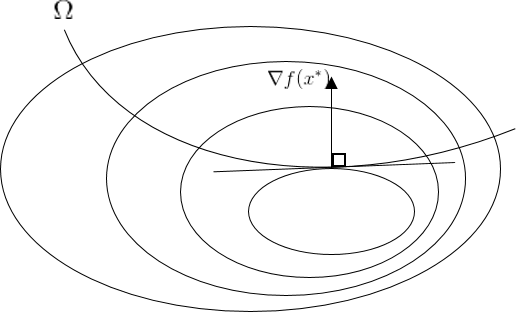
proof of Theorem F-1
Suppose not, i.e. there exists a feasible direction $d \in \mathbb{R}^n$ such that
\[\langle \nabla f(x^*), d \rangle = -\delta < 0\]Let $g(x) \triangleq \langle \nabla f(x), d \rangle$, then $g(x)$ is a continuous function, since $\nabla f(x)$ is continuous
그러면 부정의 가정에서
\[g(x^*) = -\delta\]From the assumption of continuous differential condition,
\[\exists \varepsilon > 0 \;\; \textit{such that}\;\; \left\| x - x^* \right \| < \varepsilon \implies g(x) \leq -\frac{\delta}{2}\](많이 사용하는 증명 테크닉이며 이렇게 되면 $\left| g(x) - g(x^*) \right| \leq \frac{\delta}{2}$)
and by the same assumption,
\[f(x^* + \lambda d) - f(x^*) = \int_0^1 \langle \nabla f(x^* + s \lambda d), \lambda d \rangle ds\]for some sufficiently small $\bar{\lambda} > 0$, it is satisfied that
\[x^* + \lambda d \in B^o(x^*, \varepsilon) \cap \Omega \implies g(x^* + s \lambda d) < -\frac{\delta}{2} \;\; \forall s \in [0,1]\](즉, $s=1$ 이면, $\left| g(x) - g(x^) \right| \leq \frac{\delta}{2}$ 이므로 $g(x^ + s \lambda d) < -\frac{\delta}{2}$ 이 $\varepsilon$ 보다 작은 $\lambda d$ 에서의 최대 값이다. )
정의에 의해
\[g(x^* + s \lambda d) = \langle \nabla f(x^* + s \lambda d), \lambda d\rangle \;\;\forall \lambda \in [0, \bar{\lambda}]\]이므로,
\[\begin{align} f(x^* + \lambda d) - f(x^*) &= \int_0^1 \langle \nabla f(x^* + s \lambda d), \lambda d \rangle ds < \langle \nabla f(x^* + \lambda d), \lambda d \rangle \int_0^1 ds \\ &= g(x^* + s \lambda d) \leq -\frac{\delta}{2} \end{align}\]Hence,
\[\begin{align} f(x^* + \lambda d) - f(x^*) < -\frac{\delta}{2} < 0, \;\; \forall \lambda \in [0, \bar{\lambda}] \implies f(x^* + \lambda d) < f(x^*) \end{align}\]which contradicts to the fact that $x^*$ is local minima.
Note : Brief of the first order necessary condition
\[x^* \;\; \textit{Local minimum point} \;\; \implies \;\; \langle \nabla f(x^*), h \rangle \geq 0 \;\; \forall h : \textit{Feasible Direction}\]Corollary T-1
Let $x \in \Omega \;\; \textit{&} \;\; f : \mathbb{C}^1 \rightarrow \mathbb{R}$. If $x^$ is a local minimum point of $f$ over $\Omega$ and If $x^ \in \int(\Omega)$ then $\nabla f(x^) = 0$ (Since, $\langle \nabla f(x^), h \rangle \geq 0, \;\; \forall h \in \mathbb{R}^n $)
Note
- 간단히 말하면 $\nabla f(x) = 0$, 이것이 First Order Necessary Condition
- 따름정리의 증명은 간단하다. 만일, 아니라고 하면 즉, $\nabla f(x) \neq 0$ 이면, $h$ 이 Feasible 이므로 Let $h = - \nabla f(x)$ 놓으면 간단히 가정에 위배…
Theorem F-2
Suppose that $f$ is twice continuosly differentiable. Let $\hat{x}$ is a local minimizer of $\min_{x \in B^o(\hat{x}, \rho)} f(x)$. Let $H = \frac{\partial^2 f}{\partial x^2}$ then $\langle h, H(\hat{x})h \rangle \geq 0, \;\; \forall h \in \mathbb{R}^n$.
Proof of Theorem F-2
Since $\hat{x}$ is a minimizer over $B^o(\hat{x}, \rho)$ then for any $h \in \mathbb{R}^n$
\[f(\hat{x} + \lambda h) - f(\hat{x}) = \langle \nabla f(\hat{x}), \lambda h \rangle + \int_0^1 (1-s)\langle \lambda h, H(\hat{x}+s \lambda h) \lambda h \rangle ds \;\; \textit{for} \;\; \lambda \in [0, \bar{\lambda}], \;\; \textit{some}\;\; \bar{\lambda} > 0\](다시말해 $\bar{\lambda} \left| h \right| < \rho $, $\hat{x} \in B^o(\hat{x}, \rho)$ 이므로) 결국,
\[\int_0^1 (1-s)\langle h, H(\hat{x}+s \lambda h) h \rangle ds > 0\]임을 증명해야 한다. Let $\lambda \downarrow 0$,
\(\langle h, H(\hat{x})h \rangle \int_0^1 (1-s)ds = \frac{1}{2} \langle h, H(\hat{x})h \rangle \geq 0\) Q.E.D. of Thorem F-2
Note.
즉, $x^*$ is Local Minimum 이면
First order optimality conditions
$\langle \nabla f(x^*), h \rangle \geq 0, \;\; h \textit{: : Feasible }$
Second order optimality conditions
$\langle h, H(x^*) h \rangle \geq 0, \;\; h \textit{: : Feasible }$
Theorem F-3 (Sufficient Condition)
Suppose that $f$ is twice differential continously differentiable, and that
\[\hat{x} \in \mathbb{R}^n \;\;\textit{such that}\;\; \nabla f(\hat{x}) = 0 \; \textit{and}\; H(\hat{x}) > 0\]Then $\hat{x}$ is a local minimizer of $f$.
Proof Theorem F-4
Suppose not, i.e. $\hat{x}$ is not a local minimizer of $f$, then
\[\exists \{x_i \}_{i=0}^{\infty} \;\;\textit{such that}\;\; x_i \rightarrow \hat{x}, \;\; f(x) < f(\hat{x}), \;\; \forall i \in \mathbb{N}\]( $\hat{x}$ is minimizer 가 아니므로 $f(x) < f(\hat{x})$ )
\[f(x_i) - f(\hat{x}) = \langle \nabla f(\hat{x}), x_i - \hat{x} \rangle + \int_0^1 (1-s) \langle x_i - \hat{x}, H(x + s (x_i - \hat{x})(x_i - \hat{x}) \rangle ds\]Since $H(\hat{x}) > 0$
\[\exists m > 0, \;\;\textit{such that}\;\; \langle h, H(\hat{x})h \rangle \geq m \left\| h \right\|^2\]Let $g(x) = \langle h, H(x)h \rangle$, where $g$ is continuous, since $H$ is continuous. Thus,
\[g(\hat{x}) \geq m \left\| h \right\|^2 \implies \exists \varepsilon > 0, \;\;\textit{such that}\;\; g(x) \geq \frac{m}{2} \left\| h \right\|^2, \; \forall x \in b^o(\hat{x}, \varepsilon) \tag{1}\]Since
\[x_i \rightarrow \hat{x}, \;\; \exists i_0 \;\;\textit{such that}\;\; \left\| x_i - \hat{x} \right\| < \varepsilon, \; \forall i \geq i_0\]이는 다시말해,
\[\hat{x} + s (x_i - \hat{x}) \in B^o(\hat{x}, \varepsilon), \;\; \forall i \geq i_0\]그러므로
\[\int_0^1 (1-s)g(\hat{x} + s (x_i - \hat{x})) ds \geq \frac{m}{2} \left\| h \right\|^2 \int_0^1 (1-s)ds = \frac{m}{4} \left\| h \right\|^2 > 0\](식 (1) 에서, $g(\hat{x} + s (x_i - \hat{x})) \geq \frac{m}{2}$)
\[\therefore \;\; f(x_i) - f(\hat{x}) > 0 \implies f(x_i) > f(\hat{x})\]It contradixts to the assunption (=$f(x) < f(\hat{x})$).
Theorem F-4
Suppose that $f:\mathbb{R}^n \rightarrow \mathbb{R}$ is continuously differentiable and convex. If $\hat{x} \in \mathbb{R}^n$ is such that $\nabla f(\hat{x}) = 0$, then $\hat{x}$ is a global minimizer of $f$
proof of Theorem F-4
We have proved that if $f$ is convex then $\forall x, y \in \mathbb{R}^n$
\[f(x) - f(y) \leq \langle \nabla f(y), x - y \rangle\]is satisfied. (Convex 정의에서는
\[f(y) - f(x) \leq \langle \nabla f(x), y - x \rangle\])
Let $y$ be $\hat{x}$. Then
\(f(x) - f(\hat{x}) \geq \langle \nabla f(\hat{x}), x - \hat{x} \rangle = 0 \;\;\forall \lambda \in \mathbb{R}^n \implies f(x) \geq f(\hat{x})\) Q.E.D. of Theorem F-4
Theorem F-5
Suppose that $f: \mathbb{R}^n \rightarrow \mathbb{R}$ is twice continuosly and that
\[\exists m > 0 \;\;\textit{such that}\;\; \forall x \in \mathbb{R}^n, h \in \mathbb{R}^n, \;\; \langle h, H(x)h \rangle \geq m \left\| h \right\|^2 \;\;\textit{where}\;\; H = \frac{\partial^2 f}{\partial x^2}\]Then $f(\cdot)$ has a unique minimizer. Moreover, if $f$ has a global minimizer, it has to be unique.
proof of Theorem F-5
The fact that $H(x)$ is a positive definite matrix implies that $f$ is strictly convex (Theorem F-2) If $f$ has a global minimizer, it has to be unique.
Lemma F-5
Strictly Convex에서는 Global Minima는 2개 일 수 없다. (Theorem F-5의 첫번쨰 명제 증명)
Proof of Lemma F-5
Suppose not .i.e. $\exists x^* \neq x^{}$, which are global minimizer of $f$. Then, it implies that $f(x^*) = f(x^{})$. Since $f$ is convex, it satisfies the following inequlity:
\[f(\lambda x^* + (1-\lambda)x^{**}) < \lambda f(x^*) + (1-\lambda)f(x^{**}) = f(x^*) \;\;\because f(^*) = f(x^{**})\]그러므로 $x^*$는 global minimizer 일 수 없다. 이는 가정에 위배 Q.E.D. of Lemma F-5
Need to prove that $f$ has a global minimizer. In order to prove this, we should show that for any $x_o \in \mathbb{R}^n$, the level set
\[L \triangleq \{ x \in \mathbb{R}^n | f(x) \leq f(x_o)\}\]is compact. (global minimizer의 증명에는 이것으로 충분. 즉, Strictly Convex 이면 Lemma에서 unique한 Minimizer가 존재한다. 그런데, 이것이 $\mathbb{R}^n$ 에서 global minimizer이라는 것을 증명해야 하므로..)
Proof of Closed
Let ${ x_i }_i^{\infty} \supset L$ be any converging sequence in $L$ such that $x_i \rightarrow \hat{x}$. It needs to prove that $\hat{x} \in L$, such that $f(x_i ) \leq f(x_o)\;\;\forall i \in \mathbb{Z}$. Since $f$ is continuous and $x_i \rightarrow \hat{x}$ as $i \rightarrow \infty$. Thus $f(x_i) \rightarrow f(\hat{X})$ as $i \rightarrow \infty$. ($f$가 continuous이기 때문에 ${ x_i }_i^{\infty} \supset L$ 가 convergence sequence 이면 $f$도 convergence이다.) Since $f(x_i) \leq f(x_o), \;\; f(\hat{x}) \leq f(x_o)$, for $\hat{x} \in L, \;\; \forall i$.
(만일 아니라면, 즉, $f(\hat{x}) > f(x_o)$ 이라면, Let $\delta = f(\hat{x}) - f(x_o) > 0$. and
\[\exists i_o \;\;\textit{such that}\;\; \forall i \geq i_o, \;\; f(x_i) \in B^o(f(\hat{x}), \frac{\delta}{2})\]에 대하여
\[f(x_i) - f(x_o) = f(x_i) - f(\hat{x}) + f(\hat{x}) -f(x_o) > -\frac{\delta}{2} + \delta > 0\]It implies that $f(x_i) > f(x_o)$. It contradicts to the $f(x_i) \leq f(x_o)$)
Proof of Bound
$\forall x \in L$,
\[\begin{align} 0 \geq f(x) - f(x_o) &= \langle \nabla f(x_o), x - x_o \rangle + \int_0^1 (1-s) \langle x- x_o, H(x+s(x-x_o))(x-x_o) \rangle ds \\ & \geq -\left\| \nabla f(x_o) \right\| \left\| x-x_o \right\| + \frac{1}{2}m \left\| x - x_o \right\|^2 \\ & = \left\| x -x_o \right\| (\frac{1}{2} m \left\| x - x_o \right\| - \left\| \nabla f(x_o) \right\|) \end{align}\]여기서,
- $-\left| \nabla f(x_o) \right| \left| x-x_o \right|$ 는 $\langle \nabla f(x_o), x - x_o \rangle$ 의 최소값이다.
- $\frac{1}{2}m \left| x - x_o \right|^2$ 는 Theorem의 가정이다. $\langle h, H(x)h \rangle \geq m \left| h \right|^2$ )
위 식에서
\[\left\| x -x_o \right\| (\frac{1}{2} m \left\| x - x_o \right\| - \left\| \nabla f(x_o) \right\|) \leq 0\]이어야 하므로 여기에서
\[\left\| x - x_o \right\| \leq \frac{2}{m} \left\| \nabla f(x_o) \right\|\;\;\therefore L \;\;\textit{is bound}\]Q.E.D. of Theorem F-5
Comments