- Steepest Descent Algorithm.
- Armijo Gradient Algorithm
- Rate of Convergence (worst case)
- The rate of convergence of Armijo’s Algorithm
Steepest Descent Algorithm.
\(\textit{Problem: } \;\; \min_{x \in \mathbb{R}^n} f(x)\)
| Procesdure | Processing |
|---|---|
| Data | $x_o \in \mathbb{R}^n$ |
| Step 0 | Set $i=0$ |
| Step 1 | Compute the Steepest Desvemt Direction |
| $ h_i = h(x_i) = -\nabla f(x_i)$ | |
| Stop If $\nabla f(x_i) = 0$ | |
| Step 2 | Compute the Step Size |
| * | $\lambda_i = \lambda(x_i) = \arg \min_{\lambda \geq 0} f(x_i + \lambda h_i)$ |
| Step 3 | Update $x_{i+1} = x_i + \lambda_i h_i$ replace $i $ by $i+1$ and goto Step 1 |
여기에서 Step 2는 실제로 Implementation 할 수 없다. (할 수 있는 것 처럼 보이지만, 해당 문제를 푸는 것이 Problem을 푸는 것과 같은 것)
Theorem G-1
Let \(\{ x_i \}^n_{i=0}\) be a sequence constructed by the algorithm. Then, every accumulation point $\hat{x}$ of \(\{ x_i\}_{i=0}^{\infty}\) satisfies that $\nabla f(\hat{x}) = 0$
proof of Theorem G-1
Suppose not i.e. $x_i \overset{\mathbb{K}}{\rightarrow} \hat{x}$ as $i \overset{\mathbb{K}}{\rightarrow} \infty$ but $\nabla f(\hat{x}) \neq 0$ From the definition of directional derivative, We can obtain
\[df(\hat{x}, h(\hat{x})) = - \left\| \nabla f(\hat{x}) \right\|^2 = \langle \nabla f(\hat{x}), h(\hat{x}) \rangle < 0\;\; \because h(\hat{x}) = -\nabla f(\hat{x})\]It imples that
\[\exists \delta > 0, \;\; \exists \hat{\lambda} \in \lambda(\hat{x}) \;\;\textit{such that}\;\; f(\hat{x}+\hat{\lambda}h(\hat{x})) - f(\hat{x}) = -\delta < 0\]Since $f(\cdot)$ is continuous, \(\{x_i \}_{i=0}^n\), and $\nabla f(\cdot) = h(\cdot)$ is continuous, $\exists i_o \in \mathbb{K}$ such that
\[\left\| f(x_i + \hat{\lambda}h(x_i)) - f(\hat{x} + \hat{\lambda} h(\hat{x})) \right\| \leq \frac{\delta}{4}\]and
\[\left\| f(x_i) - f(\hat{x}) \right\| \leq \frac{\delta}{4} \;\;\forall i \geq i_a\]then, since
\[f(x_i + \hat{\lambda} h(x_i)) - f(x_i) \geq f(x_{i+1}) - f(x_i)\](왜냐하면 $f(x_{i+1}) = f(x_i + \lambda h(x_i)) \leq f(x_i + \hat{\lambda} h(x_i))$, since $\lambda = \arg \min f(x_i + \lambda h(x_i))$.)
\[f(x_i + \hat{\lambda} h(x_i)) - f(x_i) = f(x_i + \hat{\lambda} h(x_i)) - f(\hat{x} + \hat{\lambda} h(\hat{x})) + f(\hat{x} + \hat{\lambda} h(\hat{x})) - f(\hat{x}) + f(\hat{x}) - f(x_i) \\ \leq \frac{\delta}{4} - \delta + \frac{\delta}{4} = -\frac{\delta}{2} < 0, \;\;\forall i \geq i_0, \;\; i \in \mathbb{K}\]( Since
\[\begin{align} f(x_i + \hat{\lambda} h(x_i)) - f(\hat{x} + \hat{\lambda} h(\hat{x})) &\leq \frac{\delta}{4} \\ f(\hat{x} + \hat{\lambda} h(\hat{x})) - f(\hat{x}) &\leq -\delta \\ f(\hat{x}) - f(x_i) &\leq \frac{\delta}{4} \end{align}\]
.)
Thus $\left| f(x_{i+1}) - f(x_i) \right| > \frac{\delta}{2}$ implies that $f(x_i) \rightarrow \infty$ 이는 가정에 모순.
Q.E.D of Theorem G.2
Armijo Gradient Algorithm
| Procesdure | Processing |
|---|---|
| Data | $x_o \in \mathbb{R}^n$, $\alpha, \beta \in (0,1)$ |
| Step 0 | Set $i=0$ |
| Step 1 | Compute the Descent Direction |
| $ h_i = h(x_i) = -\nabla f(x_i)$ | |
| Stop If $\nabla f(x_i) = 0$ | |
| Step 2 | Compute the Step Size rule |
| * |  |
| Step 3 | Update $x_{i+1} = x_i + \lambda_i h_i$ replace $i $ by $i+1$ and goto Step 1 |
Note : Core Idea
The following rule of adaptation gain is the key idea of Armijo’s algorithm
\[\lambda_i = \lambda(x_i) \triangleq \arg \max_{k \in \mathbb{N}} \{ \beta^k | f(x_i + \beta^k h_i) - f(x_i) \leq - \beta^k \cdot \alpha \left\| \nabla f(x_i) \right\|^2 \}\]Let $\phi(\lambda) = f(x + \lambda h(x)) - f(x)$ $\phi(0) = 0$ $\phi’(0) = - \left| \nabla f(x) \right|^2 |_{x=0}$
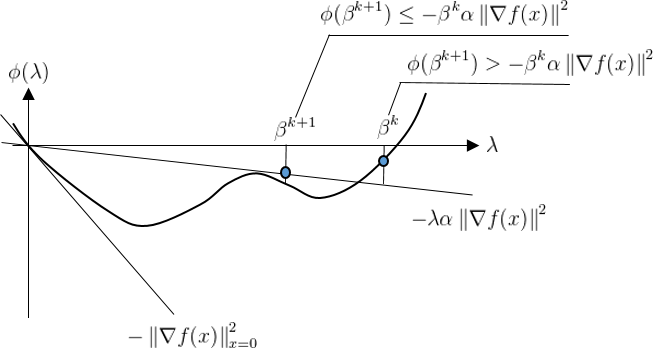
Assumption
$f$ is twice continuously differentiable and
\[\left\| H(x) \right\| \triangleq \max \{ \left\| H(x)y \right\| | \left\| y \right\| = 1 \} \leq M < \infty, \;\; \forall x \in \mathbb{R}^n\]where $H(x) = \frac{\partial^2 f(x)}{\partial x^2}$.
Theorem AG-1
Suppose that the assumption holds then,
- The Armijo step size rule is well defined.
- If \(\{ x_i \}_{i=0}^{\infty}\) is an infinite sequence constructed by the algorithm, every accumulation point $\hat{x}$ of \(\{ x_i \}_{i=0}^{\infty}\) satisfies $\nabla f(\hat{x}) = 0$
- If the set \(\{ x \in \mathbb{R}^n \| \nabla f(x) = 0 \}\) contains only a finite number of points, then any bounded sequence \(\{ x_i \}_{i=0}^{\infty}\) must converge to a point $\hat{x}$ such that $\nabla f(\hat{x}) = 0$. (Uniqueness)
- If \(x^* \neq x^{**}\) are two accumulation points of the sequence \(\{ x_i \}_{i=0}^{\infty}\) then $f(x^*) = f(x^{**})$.
Proof of Theorem AG-1
proof of well defined
In other words, it need to prove that
\[\exists \bar{K} < \infty \;\;\textit{such that}\;\; \forall i, K_i \leq \bar{K}\](즉, 유한한 Iteration으로 $\beta^{K_i}$가 수렴한다는 의미)
Let $\nabla f(x_i) \neq 0$. 일떄
\[f(x_i + \lambda h_i) - f(x_i) + \lambda \alpha \left\| \nabla f(x_i) \right\|^2 \leq 0 \;\;\textit{for} \;\;\lambda = \beta^{K_i}\]이므로, 위 식을 전개하면
\[\begin{align} &f(x_i + \lambda h_i) - f(x_i) + \lambda \alpha \left\| \nabla f(x_i) \right\|^2 \\ &= \langle \nabla f(x_i), \lambda h_i \rangle + \int_0^1 (1-s) \langle \lambda h_i, H(x_i + s \lambda h_i) \lambda h_i \rangle ds + \lambda \alpha \left\| \nabla f(x_i) \right\|^2 \\ &\leq -\lambda (1-\alpha) \left\| \nabla f(x_i) \right\|^2 + \frac{1}{2}M \lambda^2 \left\| \nabla f(x_i) \right\|^2 \\ &= \lambda \left\| \nabla f(x_i) \right\|^2 (\frac{M}{2}\lambda - (1 - \alpha)) \end{align}\]if $\lambda \in (0, \frac{2(1-\alpha)}{M})$, then $f(x_i + \lambda h_i) - f(x_i) + \lambda \alpha \left| \nabla f(x_i) \right|^2 \leq 0$, $\forall i$. 그러므로,
$\exists \bar{K}$ such that $\beta^{\bar{K}-1} \geq \frac{2(1-\alpha)}{M}$, and $\beta^{\bar{K}} \leq \frac{2(1-\alpha)}{M}$.
It implies that $\beta^{K_i} \geq \beta^{\bar{K}} \Rightarrow K_i \leq \bar{K} \;\;\forall i$. 즉, $K_i$ 는 Upperbound를 가진다.
proof of accumulation point
Suppose not i.e. $\nabla f(\hat{x}) \neq 0$, then $\exists \hat{K}$ such that $\hat{\lambda} = \beta^{\hat{K}}$ such that
\[f(\hat{x} + \hat{\lambda}h(\hat{x})) - f(\hat{x}) \leq - \hat{\lambda} \alpha \left\| \nabla f(\hat{x} )\right\|^2\]Since $\nabla f(x)$ is continuous,
\[\exists i_0 \in \mathbb{N} \;\;\textit{such that}\;\; \left\| \nabla f(x_i) \right\|^2 \geq \frac{1}{2} \left\| \nabla f(\hat{x}) \right\|^2 \;\;\forall i > i_0\] \[\begin{align} f(x_{i+1}) - f(x_i) &\leq - \lambda_i \alpha \left\| \nabla f(x_i) \right\|^2 \;\;\because \lambda_i = \beta^{K_i} \geq \beta^{\bar{K}} \\ & \leq - \beta^{\bar{K}} \alpha \frac{1}{2} \left\| \nabla f(x_i) \right\|^2 \\ & \leq - \beta \alpha \frac{1-\alpha}{M} \left\| \nabla f(x_i) \right\|^2 = -\delta < 0 \end{align}\]즉, 만일, $\nabla f(\hat{x}) = 0$ 이면 $\hat{x}$는 Accumulation point가 되지만, $\nabla f(\hat{x}) \neq 0$ 이면 $\left| f(x_{i+1}) - f(x_i) \right| \leq \delta$ 가 되어 알고리즘이 발산한다. 이는 가정에 위배.
proof of uniqueness
Without loss of generality, Assume that there exists two points $x^*$ and $x^{**}$ in the set. Since we assume that the sequence is bounded, there are accumulation points, and from (2), accumulation point satisfy $\nabla f(\hat{x}) = 0$. Hence, the sequence \(\min \{\left\| x_i - x^* \right\|, \left\| x_i - x^{**} \right\| \} \rightarrow 0\) as $i \rightarrow \infty$. (If not, there is another accumulation point which contradicts to our assumption)
Let $\rho > 0$ such that \(\rho < \frac{\left\| x^* - x^{**} \right\|}{4}\).
\[\exists i_0 \in \mathbb{N} \;\;\textit{such that}\;\; \min \{\left\| x_i - x^* \right\|, \left\| x_i - x^{**} \right\| \} < \rho\;\;\forall i \geq i_0\]i.e.
\[x_i \in B^o(x^*, \rho) \;\;\textit{or}\;\; x_i \in B^o (x^{**}, \rho)\]Since $\nabla f(x_i) \rightarrow 0$ as $i \rightarrow \infty$
\[\left\| x_{i+1} - x_i \right\| = \lambda_i \left\| f(x_i) \right\| \rightarrow 0 \;\;\textit{as}\;\; i \rightarrow \infty \;\;\because x_{i+1} = x_i + \lambda_i \nabla f(x_i)\]then
\[\exists i_1 \geq i_0 \;\;\textit{such that}\;\; \left\| x_{i+1} - x_i \right\| < \rho \;\;\forall i \geq i_1\]Suppose that $x_i \in B^o (x^, \rho)$ then $x_{i+1} \in B^o(x^, \rho)$. 여기에서
\[\begin{align} \left\| x_{i+1} - x_i \right\| &= \left\| x_{i+1} - x^{**} + x^{**} - x^* + x^* - x_i \right\| \\ &\geq \left\| x^{**} - x^* \right\| -\left\| x_{i+1} - x^{**} \right\| - \left\| x^* - x_i \right\| \\ &\geq 4\rho - \rho - \rho = 2\rho \end{align}\](두번쨰 부등식은 삼각 부등식의 응용이다. 가장 큰 값에서 다른 값을 뺀 것 보다 크다.) 이는 가정 ($\left| x_{i+1} - x_i \right| < \rho$)에 위배.
proof of 4.
\(\{ f(x_i)\}_{i=0}^{\infty}\) is a monotone decreasing sequence, then if there exists two accumulation points \(x^*, x^{**}\), \(f(x^*) = f(x^{**})\) (이미 Uniqueness 증명에서 증명된 것임)
Q.E.D. of Theorem GA-1
Exercise 1
Let $f(x)=e^{-\left|x \right|^2}$ with $x \in \mathbb{R}^n$ shows that, for this function, the Armijo gradient descent algorithm method construct the sequence \(\{ x_i \}_{i=0}^{\infty}\) such that
\[\left\| x_i \right\| \rightarrow \infty \;\; \textit{and} \;\; f(x_i) \rightarrow 0 \;\;\textit{as}\;\; i \rightarrow \infty\]Exercise 2
Consider the dunction $f(x) = x^2 e^{-x} - x$ With $x \in \mathbb{R}$. Determining the behavior of the Armijo gradient method on this functionwhen $x_0 = 0.5$ and $x_0 = 2$.
Rate of Convergence (worst case)
Definition G-1
We say that a sequence ${ x_i }_{i=0}^{\infty} \subset \mathbb{R}^n$ converge to a point $\hat{x}$ at least with rate $r \geq 1$ if
\[\exists M \in (0, \infty), \;\; \delta \in (0, \infty) \;\; \textit{and} \;\; i_0 \in \mathbb{N}\]such that
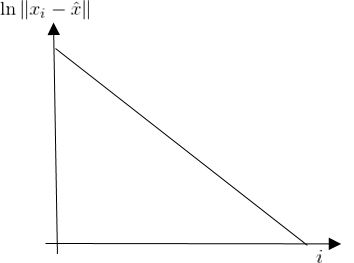
\[\forall i \geq i_0 \;\; \begin{align} &\left\| x_i - \hat{x} \right\| \leq M \delta^i \;\; \textit{if} \;\; r = 1\\ &\left\| x_i - \hat{x} \right\| \leq M \delta^{r^i} \;\; \textit{if} \;\; r > 1 \end{align}\]when $r=1$ we say that the convergence is linear and $r>1$, the convergence is super linear. ($\ln \left| x_i - \hat{x} \right| \leq \ln M\delta^i = \ln M + i \ln \delta$ : Convergence is Linear to $i$ and $\ln \left| x_i - \hat{x} \right| < \ln M + r^i \ln \delta$ : Convergence is Super Linear to $i$)
| Linear Case | Super Linear Case |
|---|---|
 |
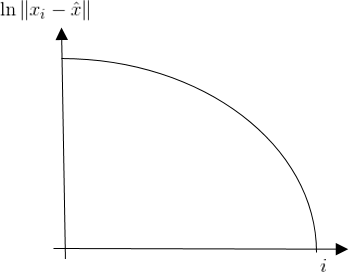 |
Note
A sequence ${ x_i }_{i=0}^{\infty}$ can converge slower than linear ex) $\left| x_i - \hat{x} \right| \leq \frac{M}{i}$
- Complexity $O(n^2)$ for $\mathbb{R}^n$ … 전체 Iteration당 계산량
- Efficiemtly … 1 Iteration당 계산량
Theorem AG-2
Let \(\{ x_i \}_{i=0}^{\infty} \subset \mathbb{R}^n\)
- If $\exists \delta \in (0,1)$ and $i_0 \in \mathbb{N}$ such that $\left| x_{i+1} - x_i \right| \leq \delta \left| x_i x_{i-1} \right| \;\; \forall i \geq i_0 + 1$ then $ \exists \hat{x} \in \mathbb{R}^n$ such that $ x_i \rightarrow \hat{x}$ as $i \rightarrow \infty$ at least linearly.
- $\exists’ M < \infty, \; r>1$ and $i_0 \in \mathbb{N}$ such that $M^{\frac{1}{r-1}} \left| x_{i_0+1} - x_{i_0} \right| < 1$ and $\left| x_{i+1} - x_i \right| \leq M \left| x_i - x_{i-1} \right|^r, \;\; \forall i \geq i_0 + 1$, then $\exists \hat{x}$ such that $x_i \rightarrow \hat{x}$ as $i \rightarrow \infty$ with root rate at least $r$.
Proof of Theorem AG-2
Proof of 1.
목표 및 증명 단계
\[\begin{align} \left\| x_i -\hat{x} \right\| \leq M \delta^i \;\; &\textit{If}\;\; r=1 \\ \left\| x_i -\hat{x} \right\| \leq M \delta^{r^i} \;\; &\textit{If}\;\; r>1 \end{align}\]- $\hat{x}$ 존재 증명
- $M, \delta$ 존재 증명 -> 목표 증명
Let $e_i = \left| x_{i+1} - x_i \right|$ then by assumption,
\(\begin{align} e_{i_0 + 1} &\leq \delta e_{i_0} \\ e_{i_0 + 2} &\leq \delta e_{i_0+1} \leq \delta^2 e_{i_0} \\ \cdots \\ e_{i} &\leq \delta^{i - i_0} e_{i_0} \;\; \forall i \geq i_0 \end{align}\) for any $j > k \geq i_0$ \(\begin{align} \left\| x_j - x_k \right\| &= \left\| x_j - x_{j+1} + x_{j+1} \cdots - x_{k+1} + x_{k+1} - x_k \right\| \\ &\leq \sum_{i=k}^{j-1} \left\| x_{i+1} - x_i \right\| = \sum_{i=k}^{j-1} e_i \leq \sum_{i=k}^{j-1} \delta^{i - i_0} e_i \leq \delta^{k - i_0} e_{i_0} \sum_{i=0}^{\infty} \delta^i \\ &= \delta^{k-i_0} e_{i_0} \frac{1}{1 - \delta} \end{align}\)
as $k \rightarrow \infty$, $\left| x_j - x_k \right| \rightarrow 0$ for any $j > k> i_0$. It implies that ${x_i }_{i=0}^{\infty}$ is Causchy Sequence. It imples again that $\exists$ a limit point $\hat{x}$ such that $x_i \rightarrow \hat{x}$ as $i \rightarrow \infty$. Then, Let $j \rightarrow \infty$. SInce $x_j \rightarrow \hat{x}$,
\[\left\| \hat{x} - x_k \right\| \leq \delta^{k-i_0} e_{i_0} \frac{1}{1 - \delta} = \frac{e_{i_0} \delta^{-i_0}}{1 - \delta} \delta^k\]Proof of 2.
Let $e_i = \left| x_{i+1} - x_i \right|$, then by assumption, $e_{i+1} \leq M e_i^r, \;\; \forall i \geq i_0$. Multiply $M^{\frac{1}{r-1}}$ both sides, i.e.
\[M^{\frac{1}{r-1}} e_{i+1} \leq M^{\frac{1}{r-1}} \cdot M e_i^r = (M^{\frac{1}{r-1}} e_i)^r\]Let $\mu_i = M^{\frac{1}{r-1}} e_i $ then $\mu_{i+1} \leq \mu_i^r \Rightarrow \ln \mu_{i+1} \leq r \ln \mu_i$ Let $w_i = \ln \mu_i$ then $w_{i+1} \leq r w_i$
\[\forall i \geq i_0, \;\; w_i \leq r^{i - i_0} w_{i_0}\]or
\[\ln \mu_i \leq r^{i - i_0} \ln \mu_{i_0} = \ln \mu^{r^{i - i_0}}\]그러므로
\[\mu_{i_0}^{r^{i - i_0}} = \mu_{i_0}^{(\frac{1}{r})^{i_0} \cdot r^i } = \left( \mu_{i_0}^{(\frac{1}{r})^{i_0} } \right)^{r^i} \;\; \forall i \geq i_0\]Since $\mu_i = M^{\frac{1}{r-1}} e_i$
\[e_i = M^{\frac{-1}{r-1}} \mu_i = \left( \frac{1}{M} \right)^{\frac{1}{r-1}} \mu_i \leq \left( \frac{1}{M} \right)^{\frac{1}{r-1}} \left( \mu_{i_0}^{(\frac{1}{r})^{i_0} } \right)^{r^i} = \left( \frac{1}{M} \right)^{\frac{1}{r-1}} \left( (M^{\frac{1}{r-1}} e_{i_0} )^{(\frac{1}{r^i})^{i_0}} \right)^{r^i} \;\; \forall i \geq i_0\]By assumption, $M^{\frac{1}{r-1}} \left| x_{i_0 + 1} - x_{i_0} \right| < 1$, thus,
\[\left( \frac{1}{M} \right)^{\frac{1}{r-1}} \left( (M^{\frac{1}{r-1}} e_{i_0} )^{(\frac{1}{r^i})^{i_0}} \right)^{r^i} = C \delta^{r^i}\]where $C = \left( \frac{1}{M} \right)^{\frac{1}{r-1}}$, $\delta = (M^{\frac{1}{r-1}} e_{i_0} )^{(\frac{1}{r^i})^{i_0}} $. 따라서, $e_i \leq C \delta^{r^i}$
\[\left\| x_j - x_k \right\| \leq \sum_{i=k}^{j-1} e_i \leq C \sum_{i=k}^{j-1} \delta^{r^i}\]$\exists i_0 \in \mathbb{N}$ such that $r^i - r^k \geq i - k \;\; \forall i \geq i_0 \;\; \because r > 1$ implies that $\delta^{(r^i - r^k)} \geq \delta^{i-k}$ thus,
\[\begin{align} C \sum_{i=k}^{\infty} \delta^{r^i} &\leq C \left( \sum_{i=k}^{i_0 - 1} \delta^{r^i} + \sum_{i=i_0}^{\infty} \delta^{r^i} \right) = C \delta^{r^k}\left( \sum_{i=k}^{i_0 - 1} \delta^{r^i - r^k} + \sum_{i=i_0}^{\infty} \delta^{r^i - r^k}\right) \\ &\leq C \delta^{r^k}\left( \sum_{i=k}^{i_0 - 1} \delta^{r^i - r^k} + \sum_{i=i_0}^{\infty} \delta^{i - k}\right) = C' \delta^{r^k} \end{align}\]왜냐하면, as $k \rightarrow \infty$, $\left| x_j - x_i \right| \rightarrow 0$ 따라서 Causchy Sequence. It implies that $\exists \hat{x} \in \mathbb{R}^n$ such that $x_i \rightarrow \hat{x}$ as $i \rightarrow \infty$.
Let $j \rightarrow \infty$, $\left| \hat{x} - x_k \right| \leq C’ \delta^{r^k}$. It means converge with root rate.
The rate of convergence of Armijo’s Algorithm
Assumption AG-3
$f : \mathbb{R} \rightarrow \mathbb{R}^n$ is twice continuosly differentiable, and $\exists 0 < m \leq M \infty$ such that
\[m \left\| v \right\|^2 \leq \langle v, \frac{\partial^2 f(x)}{\partial x^2} v \rangle \leq M \left\| v \right\|^2\]Theorem AG-3
Suppose that the Assumption holds. If ${x_i }{i=0}^{\infty}$ is a sequence constructed by Armijo descent algorithm in solving $\min{x \in \mathbb{R}^n} f(x)$, then
- $x_i \rightarrow \hat{x}$ as $i \rightarrow \infty$ with $\hat{x}$, the unique minimizer of $f(\cdot)$.
- $x_i \rightarrow \hat{x}$ as $i \rightarrow \infty$ Linearly with convergence rate of
where $\max 4 \alpha (1-\alpha) = 1$.
Proof of Theorem AG-3
Sketch of Proof
- By the assumption, $f$ is strictly convex and the level sets of $f(\cdot)$ is compact. $\Rightarrow \exists \hat{x}$ and it is unique.
- Need to prove that $\exists M < \infty, \delta \in (0,1)$ such that $\left| x_i - \hat{x} \right| \leq M \delta^i$
Proof of 1.
For any $x_i$,
\[\begin{align} f(x_i) - f(\hat{x}) &= \langle \nabla f(\hat{x}), x_i - \hat{x} \rangle + \int_0^1 (1-s) \langle x_i - \hat{x}, H(\hat{x}+s(x_i - \hat{x}))(x_i -\hat{x}) \rangle ds \\ &\leq \int_0^1 (1-s)M \left\| x_i - \hat{x} \right\|^2 ds \;\;\;\; \because \nabla f(\hat{x}) = 0 \end{align}\] \[\therefore \frac{1}{2}m \left\| x_i - \hat{x} \right\| \leq f(x_i) - f(\hat{x}) \leq \frac{1}{2} M \left\| x_i - \hat{x} \right\|^2 \tag{1}\]위 식에서 Strictly convex 이고 Bounded 이므로 Compact. 따라서 $\hat{x}$는 $f(x)$의 Unique Minimizer 이다.
Proof of 2.
Since $\nabla f(\hat{x}) = 0$, and by the 1st expansion $f(y)-f(x)=\int_0^1 \langle \nabla f(x+s(y-x)), y-x \rangle ds$
\[\nabla f(x_i) - \nabla f(\hat{x}) = \nabla f(x_i) = \int_0^1 H(\hat{x}+s(x_i - \hat{x}))(x_i - \hat{x}) ds\]Multiply $(x_i x^*)$ bothe sides,
\[\langle x_i - x, \nabla f(x_i) \rangle = \int_0^1 \langle x_i - x, H(\hat{x}+s(x_i - \hat{x}))(x_i - \hat{x}) \rangle ds\]By assumption,
\[m \left\| x_i - \hat{x} \right\|^2 \leq \langle x_i - \hat{x}, \nabla f(x_i) \rangle \leq \left\| \nabla f(x_i) \right\| \cdot \left\| x_i - \hat{x} \right\|\]In Armijo’s Step size rule,
\[\begin{align} f(x_i + \lambda h_i) &= f(x_i) + \lambda \alpha \left\| h_i \right\|^2 \leq \langle \nabla f(x_i), \lambda h_i \rangle + \int_0^1 \langle \lambda h_i, H(x_i + s \lambda h_i) \lambda h_i \rangle ds + \lambda \alpha \left\| h_i \right\|^2 \\ &\leq -\lambda (1 - \alpha) \left\| h_i \right\|^2 + \frac{M}{2} \left\| h_i \right\|^2 \lambda^2 \leq -\lambda \left\| h_i \right\|^2 \left( 1 - \alpha - \frac{\lambda M}{2} \right) \end{align}\]If $0 < \lambda < \frac{2(1-\alpha)}{M}$ then $-\lambda \left| h_i \right|^2 \left( 1 - \alpha \frac{\lambda M}{2} \right) \leq 0$ then
\[f(x_i + \lambda h_i) - f(x_i) \leq - \lambda \alpha \left\| \nabla f(x_i) \right\|^2\]Claim : $\lambda_i = \beta^{k_i} \geq \frac{2(1-\alpha)}{M} \beta$. 즉 앞의 가정과 달리, 이렇다고 하면
\[\lambda_i = \arg \max \{ \beta^k | f(x_i + \beta^k h_i) - f(x_i) \leq -\beta^k \alpha \left\| h_i \right\|^2 \}\]에서 Let $g(\lambda) = f(x_i + \lambda h_i) - f(x_i) + \lambda \alpha \left| h_i \right|^2$
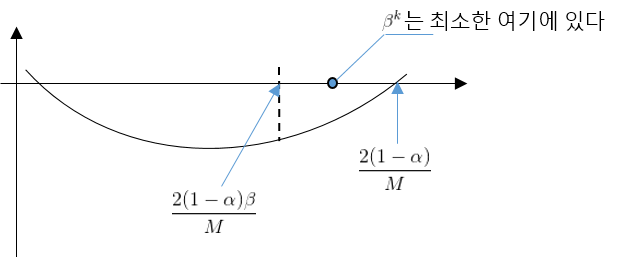 thus,
thus,
위 식의 맨 마지막 항은 다음과 같이 유도 된다. $\langle \nabla f(x_i), h \rangle + \frac{m}{2} \left| h \right|^2$ 의 최소값을 찾기 위해 $h$ 에 대하여 미분하면 $\nabla f(x_i) + mh = 0$ 에서 $h = -\frac{\nabla f(x_i)}{m}$ 를 원 식에 대입하면 $-\frac{1}{2m} \left| \nabla f(x_i) \right|^2$ 를 얻는다.
그러므로
\[\left\| \nabla f(x_i) \right\|^2 \geq 2m ( f(x_i) - f(\hat{x})) \;\;\;\; \tag{4}\]Substitute (4) into (3)
\[\begin{align} f(x_{i+1}) - f(x_i) &\leq - \frac{4m \beta \alpha (1-\alpha)}{M} (f(x_i) - f(\hat{x})) \\ f(x_{i+1}) - f(\hat{x}) + f(\hat{x}) - f(x_i) &\leq - \frac{4m \beta \alpha (1-\alpha)}{M} (f(x_i) - f(\hat{x})) \\ f(x_{i+1}) - f(\hat{x}) &\leq \left( 1- \frac{4m \beta \alpha (1-\alpha)}{M} \right)(f(x_i) - f(\hat{x})) \\ \Rightarrow f(x_i) - f(\hat{x}) \leq \delta^i (f(x_o) - f(\hat{x})) \end{align}\]From (1).
\[\frac{m}{2} \left\| x_i \hat{x} \right\|^2 \leq \delta^i (f(x_o) - f(\hat{x})) \implies \left\| x_i - \hat{x} \right\| \leq \left( \frac{2}{m} (f(x_o) - f(\hat{x})\right)^{\frac{1}{2}} \left( \delta^{\frac{1}{2}}\right)^i\]즉, $M \triangleq \left( \frac{2}{m} (f(x_o) - f(\hat{x})\right)$ and $\delta’ \triangleq \delta^{\frac{1}{2}} \;\;\; \forall i \geq 0$. 이런 식으로 하여 $\alpha$를 구할 수 있다.
Comments