\(\min_{\lambda \geq 0} \{f(x_i + \lambda h_i) \} \Rightarrow \textit{Let} \;\; \phi(\lambda)= f(x_i + \lambda h_i) - f(x_i) \Rightarrow \min_{\lambda} \phi(\lambda)\)
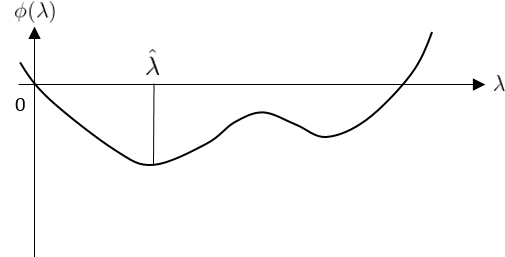
Golden Search Method
Assumption
$g(\cdot)$ is unimode i.e. $\exists \hat{\lambda}$ such that $g’(\hat{\lambda}) = 0$ (It means that there exists unique golden minimum)
Observation
- Suppose that we have additional point $a’, b’$ such that $a < a’ < b’ < b$. Either,
\(\phi(a') \leq \min \{ \phi(a), \phi(b) \} \;\;\textit{or}\;\;\phi(b') \leq \min \{ \phi(a), \phi(b) \}\)
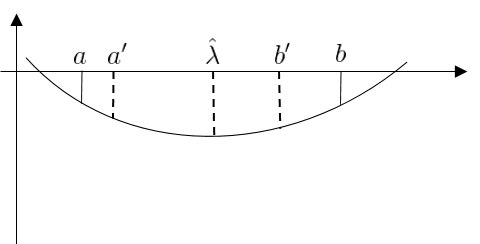
For $\phi:[a, b] \rightarrow \mathbb{R}$ and the global minimizer $\hat{\lambda} \in [a,b]$
- $[a, b] \rightarrow [X]$ What is $X$
- $X$ is smaller than $[a, b]$
- $[X] \subset [a, b]$
- $\hat{\lambda} \in [X]$
From Assumption and Observation
case 1
$\phi(a’) \leq \min { \phi(a), \phi(b)}$
- Suppose that $\phi(a’) \leq \phi(b’)$ then, by mean value theorem, $\exists \lambda_i \in [a’, b’]$ such that $\phi’(\lambda_i) \geq 0$. Since $\phi(a’) \leq \phi(a)$, by the mean value theorem $\exists \lambda_2 \in [a, a’]$ such that $\phi(\lambda_2) \leq 0$, thus
so pick $[a, b’]$ as next interval.
case 2
- Suppose that $\phi(a’) > \phi(b’)$. By the mean value theorem $\exists \lambda_1 \in [a’, b’], \; \lambda_1 \in [b, b’]$ such that $\phi’(\lambda_1) \leq 0, \; \phi’(\lambda_1) \geq 0$, ($\phi(b’) \leq \phi(b)$), Since $\hat{\lambda} \in [\lambda_1, \lambda_2$, and
pick $[a’, b]$
- Given $[a_i, b_i]$ find $a’_i, b’_i$ such that
In other words, let the small part be itself and minimize the larger part continuously 즉, 작은 쪽은 놔 두고 큰 쪽만 계속 줄여나가는 것
Golden Search Algorithm
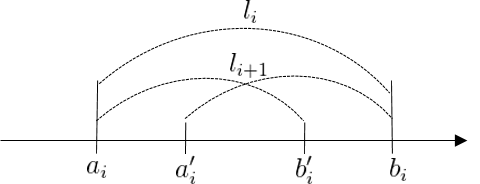 \(\begin{align}
l_{i+1} &= F l_i \;\;\; F \in (0,1) \\
l_{i+1} - (1 _F) l_i &= (1 - F) l_{i+1}
\end{align}\)
\(\begin{align}
l_{i+1} &= F l_i \;\;\; F \in (0,1) \\
l_{i+1} - (1 _F) l_i &= (1 - F) l_{i+1}
\end{align}\)
Since $(1 - F) l_i = l_i - l_{i+1}$
\[F l_i - (1-F) l_i = (1-F)F l_i \implies F - 1 + F = F - F^2 \implies F^2 + F - 1 =0, \;\; F = 0.618\]$F = 0.618 $ 에서 Golden Search
Procedure of Golden Search Algorithm
| Procesdure | Processing |
|---|---|
| Data | $x_o \in \mathbb{R}$ |
| Step 0 | Compute a bracket $[a_0, b_0]$ containing $\hat{\lambda}$, the minimizer of $\phi(\lambda)$ and Set $i=0$ (초기조건 $\phi(a_0) < 0, \phi(b_0) > 0$ |
| Step 1 | Set $l_i = b_i - a_i$ and Compute |
| $ a’_i = a_i + (1 - F) l_i$ | |
| $ b’_i = b_i - (1 - F) l_i$ | |
| Step 2 | If \(\phi(b'_i) \leq \phi(a'_i)\) set \(a_{i+1} = a'_i, b_{i+1} = b_i\) |
| else \(\phi(b'_i) > \phi(a'_i)\) set \(a_{i+1} = a_i, b_{i+1} = b'_i\) | |
| Step 3 | Set i++ and goto step 1 |
Successive Quadratic Interpolation (SQI)
\[\min_{\lambda \in \mathbb{R}_{+}} \phi(\lambda), \;\;\; \phi(\lambda) = f(x + \lambda h)\]Assumption
$\phi(\cdot)$ is continuously differentiable and unimodal with unique minimizer $\hat{\lambda}$ ($\exists \hat{\lambda} \implies \phi’(\hat{\lambda}) = 0$)
Note
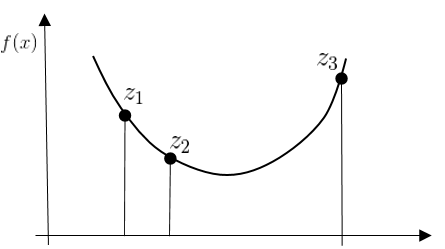
Given three distict point $z_1 < z_2 < z_3$, we can construct a inique quadaratic polynomial. \(q(\lambda) = a_1 \lambda^2 + a_2 \lambda + a_3 \;\;\textit(such that)\;\; q(z_1) = \phi(z_i) \;\; i=1,2,3\)
Largrangian Interpolation formula
\[q(\lambda) = \phi(z_1) \frac{(\lambda - z_2)(\lambda - z_3)}{(z_1 - z_2)(z_1 - z_3)} + \phi(z_2) \frac{(\lambda - z_1)(\lambda - z_3)}{(z_2 - z_1)(z_2 - z_3)} + \phi(z_3) \frac{(\lambda - z_1)(\lambda - z_2)}{(z_2 - z_1)(z_3 - z_2)}\]- Given two distict points $z_1 < z_3$ We can construct interpolating polynomial $q(\lambda)$ such that
Case 1 : $z_1 = z_2 < z_3$
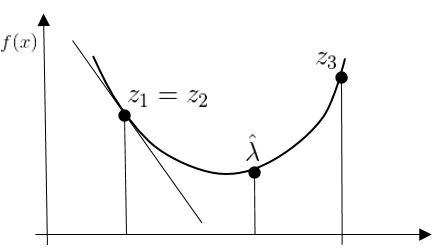
- case 1-1
- case 1-2
Case 2 : $z_1 < z_2 = z_3$
Replace $z_1$ by $z_3$ and $z_3$ by $z_1$
Conclusion
Let $z = (z_1, z_2, z_3) \in \mathbb{R}^3$, then the possible set of a vector $z$ such that $z_1 \leq \hat{\lambda} \leq z_3$ is
\[\begin{align} T &= \{ z \in \mathbb{R}^3 | \phi(z_2) \leq \min \{ \phi(z_1), \phi(z_3)\}, z_1 < z_2 < z_3 \} \\ &\cup \{ z \in \mathbb{R}^3 | z_1 = z_2 < z_3, \;\;\textit{and}\;\; \phi'(z_1) \leq 0, \;\;\textit{and}\;\; \phi(z_1) \leq \phi(z_3) \} \\ &\cup \{ z \in \mathbb{R}^3 | z_1 < z_2 = z_3, \;\;\textit{and}\;\; \phi'(z_3) \geq 0, \;\;\textit{and}\;\; \phi(z_1) \geq \phi(z_3) \} \\ &\cup \{ z \in \mathbb{R}^3 | z_1 = z_2 = z_3 = \hat{\lambda} \} \end{align}\]즉, \(q(\lambda\mid z) = q(\lambda)\mid _{(z_1, z_2, z_3)}\)
\[\hat{\lambda} = \arg \min q(\lambda|z)\]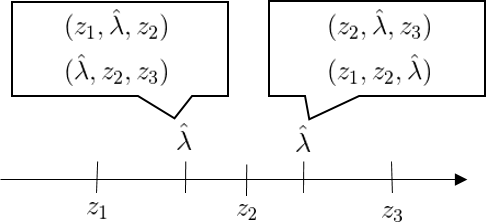
Comments