- Local Newton’s Algorithm
- Local Newton’s Method
- Global Newton Method for Convex function
- Armijo-Newton Method
Local Newton’s Algorithm
Assumption
- $f$ is twice differentiable (continulously) … Convex Condition
- Locally Lipschtz continuous … 한정된 미분치
- i.e. given any bounded set $S \subset \mathbb{R}^n$
- $\exists 0 < m \leq M < \infty$ such that $\forall y \in \mathbb{R}^n$
where $\hat{x}$ is a local minimizer.
Basic Idea
Given $f(\cdot)$, we cam approximate $f$ near $x_i$ using a taylor expansion such that
\[f(x) \approx f(x_i) + \langle \nabla f(x_i), x - x_i \rangle + \frac{1}{2} \langle x - x_i, H(x_i)(x - x_i) \rangle \tag{1}\]It is minimized at $x_{i+1} = x_i - H^{-1}(x_i)\nabla f(x_i)$ 그리고 $\nabla f(x) = 0$ 에서 식(1)을 $x$ 에 대하여 미분하면
\[\begin{align} \nabla f(x) &= \nabla f(x_i) + H(x_i) (x - x_i) \\ 0 &= \nabla f(x_i) + H(x_i) (x - x_i) \\ -\nabla f(x_i) &= H(x_i) (x - x_i) \\ x - x_i &= -H^{-1}(x_i)\nabla f(x_i) \end{align}\]Therefore, by assumption, $H(\hat{x})$ is positive definite and, since $ m \leq |x| \leq M$,
\[\exists B(\hat{x}, \rho), \;\;\textit{such that}\;\; \frac{m}{2} \|y\|^2 < \langle y, H(x) y \rangle \leq 2M \|y\|^2\]즉, Positive Definite 존재하는 지역에서만 성립.
Local Newton’s Method
| Procesdure | Processing |
|---|---|
| Data | $x_o \in \mathbb{R}$ |
| Step 0 | Set $i=0$ |
| Step 1 | Compute the search direction |
| $ h_i = -H^{-1}(x_i) \nabla f(x_i)$ | |
| Step 2 | Update $x_{i+1} = x_i + h_i$ |
| Replace $i$ by $i+1$ | |
| Step 3 | goto step 1 |
Assumption
- $H(\cdot)$ is locally Lipschitz continuous i.e.
- For a bounded set $S \subset \mathbb{R}^n$
- $\exists 0 < m \leq M < \infty$ such that
Theorem 1.
Suppose that the above assumptions are satisfied, then $\exists \hat{\rho} > 0$ such that $\forall x_0 \in B^o(\hat{x}, \hat{\rho})$, the sequence ${x_i}_{i=0}^{\infty}$ constructed by the algorithm converging to $\hat{x}$ quadratically. (i.e. by root rate 2)
proof
Since $H(\cdot)$ is continuous, $\exists \rho > 0$, and $L < \infty$ such that $\forall x \in B^o(\hat{x}, \hat{\rho})$.
\[\begin{align} \frac{m}{2}\|y\| \leq \langle y, H(x)y \rangle \leq 2 M \|y\|^2 \;\;\;\;\;\;\;\;\;& \forall y \in \mathbb{R}^n \\ \| H(x') - H(x'') \| \leq L \cdot \| x' - x'' \|, \;\;\;\;\;\;\; & x', x'' \in B^o(\hat{x}, \rho) \end{align}\]Since that $x_i \in B^o(\hat{x}, \rho)$ then
\[\begin{align} H(x_i) (x_{i+1} - x_i) &= H(x_i) \left( H^{-1}(x_i) \nabla f(x_i) \right) = - \nabla f(x_i) & \\ &= - (\nabla f(x_i) - \nabla f(\hat{x})) & \because \text{ since } \nabla f(\hat{x}) = 0 \end{align}\]Since
\[g(x_i) - g(\hat{x}) = \int_0^1 \langle \nabla g(\hat{x} + s (x_i - \hat{x})), (x_i - \hat{x}) \rangle ds\]The above equation is equal to
\[- (\nabla f(x_i) - \nabla f(\hat{x})) = -\int_0^1 \langle H(\hat{x} + s (x_i - \hat{x})), (x_i - \hat{x}) \rangle ds\]Subtract $H(x_i)\hat{x}$ from both sides
\[H(x_i) (x_{i+1} - x_i) = H(x_i) (x_{i+1} - x_i) - H(x_i)\hat{x} + H(x_i)\hat{x} = H(x_i)(x_{x_i+1} - \hat{x}) + H(x_i)(\hat{x} - x_i)\]Henceforth,
\[H(x_i)(x_{x_i+1} - \hat{x}) + H(x_i)(\hat{x} - x_i) = -\int_0^1 \langle H(\hat{x} + s (x_i - \hat{x})), (x_i - \hat{x}) \rangle ds \\ \begin{align} \Rightarrow H(x_i)(x_{x_i+1} - \hat{x}) &= \int_0^1 \left( H(x_i) - H(\hat{x} + s (x_i - \hat{x})) \right) ds (x_i - \hat{x}) \\ \Rightarrow x_{x_i+1} - \hat{x} &= H^{-1}(x_i)\int_0^1 \left( H(x_i) - H(\hat{x} + s (x_i - \hat{x})) \right) ds (x_i - \hat{x}) \\ \Rightarrow \| x_{x_i+1} - \hat{x} \| &\leq \| H^{-1}(x_i) \| \int_0^1 \| H(x_i) - H(\hat{x} + s (x_i - \hat{x})) \|ds \| x_i - \hat{x} \| \end{align}\]By the definition of the Induced norm, $|H(x)| | = \sup_{|y|=1} \langle y, H(x)y \rangle \leq 2M$, by the assumptions. Thus, $| H^{-1}(x) | \leq \frac{2}{m} $. Therefore
\[\begin{align} \| x_{x_i+1} - \hat{x} \| &\leq \frac{2}{m} \int_0^1 L \cdot \| x_i - \hat{x} - s (x_i - \hat{x}) \|ds \| x_i - \hat{x} \| \\ &= \frac{2}{m} \int_0^1 L \cdot \| (1-s)(x_i - \hat{x}) \|ds \| x_i - \hat{x} \| \\ &\leq \frac{2}{m} L \cdot \| x_i - \hat{x} \|^2 \cdot \int_0^1 (1-s) ds \\ &\leq \frac{L}{m} \| x_i - \hat{x} \|^2 \end{align}\]if $\frac{L}{m} | x_i - \hat{x} | < 1$ then, $| x_{i+1} - x_i | < | x_i - \hat{x} |$. (자승의 영향을 없앤다.)
For any $\alpha \in (0,1)$ pick $\hat{\rho} = \min(\rho, \alpha \frac{m}{L})$. Then, if $x_0 \in B^o(\hat{x}, \hat{\rho}) $, i.e.
\[\| x_0 - \hat{x} \| \leq \hat{\rho} \leq \alpha \frac{m}{L} \Rightarrow \frac{L}{m} \| x_0 - \hat{x} \| \leq \alpha < 1\]Now, we have that.
\[\begin{align} \| x_1 - \hat{x} \| &\leq \frac{L}{m} \| x_0 - \hat{x} \|^2 \leq \alpha \|x_0 - \hat{x} \| \\ \| x_2 - \hat{x} \| &\leq \frac{L}{m} \| x_1 - \hat{x} \|^2 \leq \alpha \|x_1 - \hat{x} \| \leq \alpha \|x_0 - \hat{x} \|^2 \\ \cdots \\ \| x_i - \hat{x} \| &\leq \alpha^i \| x_0 - \hat{x} \| \end{align}\]Since $\alpha \in (0,1)$, $a^i \rightarrow 0$ as $i \rightarrow \infty$. Therefore $|x_i - \hat{x} | \rightarrow 0$ as $i \rightarrow \infty$. It implies that ${x_i }_{i=0}^{\infty}$ converges to $\hat{x}$.
Is it quadratic converge? From the abovbe inequalities, we can obtain
\[\| x_{i+1} - x_i \| \leq \frac{L}{m} \| x_i - \hat{x_i} \|^2.\]Multiply $\frac{L}{m}$ both sides
\[\frac{L}{m} \| x_{i+1} - x_i \| \leq (\frac{L}{m} \| x_i - \hat{x_i} \|)^2.\]Let $\mu_i = \frac{L}{m} | x_i - \hat{x} |$ then we have
\[\mu_{i+1} \leq \mu_i^2 \Rightarrow \mu_{i+1} \leq (\mu_{i-1}^2)^2 \cdots \leq (\mu_0^2)^{i+1}\]It represents that the sequence ${x_i }_{i=0}^{n}$ converges with root rate 2, so that it calls thst quadratic converge.
Global Newton Method for Convex function
Assumption
a) $f:\mathbb{R}^n \rightarrow \mathbb{R}$ is twice continuoiusly locally Lipschitz differentiable. i.e. given any bounded set $S \subset \mathbb{R}^n$.
\[\forall x,y \in S, \;\;\exists L_s < \infty \;\;\text{ such that }\;\; \|H(x) - H(y) \| \leq L_s \| x- y \|\]b) $\exists m > 0$ such that $m |y|^2 \leq \langle y, H(x)y \rangle \;\; \forall x, y \in \mathbb{R}^n$
- 다시말해 b)는 Strictly convex를 의미함 (최소한 0은 아니기 때문에)
Proposoition
Under the condition which is mentioned in the above assumptions, a) The level set of $f(\cdot)$ is compact b) $\min f(x)$ has a unique minimizer.
Proof
a) done b) Suppose that i.e. $\exists x^*$ and $x^{**} $ 왜냐하면 일단, Convex 이므로 Compact 이다. 고로 최소한 하나의 극점은 존재한다. (Convex Set 참조) 그러므로
\[\begin{align} 0 &= f(x^{**}) - f(x^*) = \langle \nabla f(x^{**}), x^{**} - x^{*} \rangle + \int_0^1 (1-s) \langle x^{**} - x^{*}, H(x^* + s(x^{**} - x^*))(X^** - x^*) \rangle ds \\ &= \frac{1}{2} m \| x^{**} - x^* \|^2 \leq 0 \end{align}\]위 식이 만족하려면 $x^{*} = x^$ .
Armijo-Newton Method
| Procesdure | Processing |
|---|---|
| Data | $x_o \in \mathbb{R}^n$ |
| Step 0 | Set $i=0$ |
| Step 1 | Compute the search direction |
| $ h_i = -H^{-1}(x_i) \nabla f(x_i)$ | |
| Step 2 | Compute the step size |
| Step 3 | Set $x_{i+1} = x_i + \lambda_i h_i$ |
| Step 4 | Replace $i$ by $i+1$ and goto Step 1 |
- Step size for Algorithm
Theorem 2
Suppose that the assumption holds, if ${x_i}_{i=0}^{\infty}$ is a sequence constructed by the Armijo-Newton method then $x_i \rightarrow \hat{x}$ as $i \rightarrow \infty$ quadratically. where $\hat{x}$ is the unique minimizer of $f(x)$
- 여기서 Directional Derivation 과 Step-size 조건은 다음과 같다.
proof
It needs to prove that
- $x_i \rightarrow \hat{x}$ as $i \rightarrow \infty$
- Converge quadratically
proof of 1 먼저 Convergence를 증명한다. By the proposition, the level set is compact. Consider $L_0 = { x \in \mathbb{R}^n | f(x) \leq f(x_0) }$ 이때
- Strictly Convex 때문에 다음이 만족되며
- Compact 때문에 다음이 만족된다.
따라서
\[m \| y \|^2 \leq \langle y, H(x)y \rangle \leq M \| y \|^2\]이를 증명한다.
Let $h(x) = -H^{-1}(x) \nabla f(x)$ Then $H(\cdot), \nabla f(\cdot)$ are continuous by assumption.
Let \(r = \max \{f(x + \lambda h(x)) | x \in L_0, \lambda \in [0,1] \}\) then
\[g(x,y) = \langle y, H(x)y \rangle \;\;\; \text{ and } \;\; \|y\| \leq 1 \;\;\;\text{ by compact} \\ x \in L_r = \{ z \in \mathbb{R}^n | f(z) \leq r \} \;\;\;\;\;\;\;\;\;\text{ by compact}\]- 왜냐하면 $g : \mathbb{R}^n \times \mathbb{R}^n \rightarrow \mathbb{R}$ 에서 $X \subset \mathbb{R}^n$ 이 Compact 이고 $Y \subset \mathbb{R}^n$ 이 Compact이고 $M \subset \mathbb{R}$ 이 Compact 이기 떄문이다. 즉, $ g: X \times Y \rightarrow M$ . 이기 때문.
그리고 $g(x,y)$는($(x,y)$에서 continuous, 고로 $g(x,y) \leq M | y |^2$ 그러므로 \(x_i \overset{K}{\rightarrow} \hat{x}, \;\{x_i\}_{i=0}^{\infty} \subset L_r\) which is compact. It implies that there exists at least one accumulation point, i.e. ${x_i}_{i \in K}$ converges to $\hat{x}$
(왜냐하면, $f(x_i)$는 monotone decreasing sequence 이기 때문)
다음 $\nabla f(\hat{x}) = 0$ 을 증명한다.
Suppose not, i.e. $\nabla f(\hat{x}) \neq 0$, for any $x \in L_r, h(x) = - H^{-1}(x)\nabla f(x)$. 다음과 같이 놓자.
\[\begin{align} f(x + \lambda h) - f(x) - \lambda \alpha \langle h, \nabla f(x) \rangle &= \langle \nabla f(x), \lambda h \rangle - \lambda \alpha \langle h, \nabla f(x) \rangle + \int_0^1 (1-s) \langle \lambda h, H(x + s \lambda h) \lambda h \rangle ds \\ &= -\lambda (1 - \alpha) \langle \nabla f(x), H^{-1}(x)\nabla f(x) \rangle + \lambda^2 \int_0^1 (1-s) \langle h, H(x + s \lambda h) h \rangle ds \\ &\leq -\lambda (1 - \alpha) \frac{1}{M}\| \nabla f(x) \|^2 + \lambda^2 \int_0^1 (1-s) \| H^{-1}(x) \|^2 \cdot \| \nabla f(x) \|^2 \cdot \| H(x + s \lambda h) \| ds \\ & \leq -\lambda (1 - \alpha) \frac{1}{M}\| \nabla f(x) \|^2 + \frac{\lambda^2 M}{2 m^2} \| \nabla f(x) \|^2 \\ &= -\lambda \| \nabla f(x) \|^2 \left( \frac{1- \alpha}{M} - \frac{\lambda M}{2 m^2} \right) \end{align}\]여기에서
\[f(x_i + \beta^k h_i) - f(x_i) \leq \beta^k \alpha \langle h_i, \nabla f(x_i) \rangle \Rightarrow f(x_i + \beta^k h_i) - f(x_i) - \beta^k \alpha \langle h_i, \nabla f(x_i) \rangle \leq 0\]에 따라 반드시
\[\left( \frac{1- \alpha}{M} - \frac{\lambda M}{2 m^2} \right) \geq 0\]이어야 한다. 그러므로, 정의에 의해 $\lambda > 0$ 이기 떄문에 $0 < \hat{\lambda} \leq \frac{2m^2 (1 - \alpha)}{M^2}$ 인 $\hat{\lambda}$ 에 대하여
\[\forall \lambda \in (0, \hat{\lambda}], \;\; f(x_i + \lambda_i h(x_i)) - f(x_i) \leq \lambda_i \alpha \langle h(x_i), \nabla f(x_i) \rangle \tag{2}\]가 만족된다. 또한, 다음 그림과 같이 $\lambda_i \geq \beta \hat{\lambda}$ 이므로, $\lambda_i$는 상하한을 가진다.
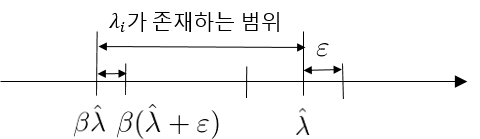
따라서, Since $\nabla f(\hat{x}) \neq 0$, i.e. $\langle h(\hat{x}). \nabla f(\hat{x}) \rangle = -\delta < 0$ (Descent 방향이므로 위와 같이 $\lambda$가 선택되어진다면 $\nabla f(\hat{x}) \neq 0$ 조건에서 식 (2)에서 당연하다.),
\[\exists i_0 \;\; \text{ such that } \;\; \langle h_i, \nabla f(x_i) \rangle \leq -\frac{\delta}{2}\]by continuity of $h(\cdot)$ and $\nabla f(\cdot)$, and $x_i \rightarrow \hat{x}$,
\[f(x_{i+1}) - f(x_i) \leq \lambda_i \alpha \langle \nabla f(x_i), h_i \rangle \leq \beta \hat{\lambda} \alpha \left( -\frac{\delta}{2} \right) < 0\]따라서 $f(x_i)$는 수렴하지 않고 발산한다. i.e. $f(x_i) \rightarrow \infty, \; \forall i \geq i_0 $ 그러므로 $\nabla f(\hat{x}) = 0$ 이다.
proof of convergence quadratically
- idea는 local newton method는 quadratically하게 수렴한다는 것을 응용
- Local Newton method
- Armijo Newton
두 알고리즘의 경우 $\lambda = 1$ 이면 같다.
Need to prove that
\[\exists i_0 \;\; \text{ such that } \;\; \forall i \geq i_0, \lambda_i = 1\]Set $\lambda = 1$ 이면
\[f(x_i + \lambda_i h_i) - f(x_i) - \alpha \langle \nabla f(x_i), h_i \rangle = \langle \nabla f(x_i), h_i \rangle + \int_0^1 (1-s) \langle h_i, H(x_i + sh_i) h_i \rangle ds - \alpha \langle \nabla f(x_i), h_i \rangle \tag{3}\]Assumptiom (a) holds : $H(\cdots)$ Locally Lipschitz continuous, i.e.
\[\| H(x') - H(x'') \| \leq L \| x' - x'' \| \;\;\; \forall x'. x'' \in S \subset \mathbb{R}^n\]where $S$ is a bounded set.
Since $x_i \rightarrow \hat{x}$ and $\nabla f(\cdot)$ is continuous, $\nabla f(x_i) \rightarrow \nabla f(\hat{x}) = 0$ then let
\[\begin{align} \langle \nabla f(x_i), h_i \rangle &= \frac{1}{2} \langle \nabla f(x_i), h_i \rangle + \frac{1}{2} \langle \nabla f(x_i), h_i \rangle \\ &= -\frac{1}{2} \langle \nabla f(x_i), H^{-1}(x_i)\nabla f(x_i) \rangle + \int_0^1 (1-s)ds \langle \nabla f(x_i), h_i \rangle \\ &= -\frac{1}{2} \langle \nabla f(x_i), H^{-1}(x_i)\nabla f(x_i) \rangle - \int_0^1 (1-s) \langle \nabla f(x_i), H^{-1}(x_i)\nabla f(x_i) \rangle ds \\ &= -\frac{1}{2} \langle \nabla f(x_i), H^{-1}(x_i)\nabla f(x_i) \rangle - \int_0^1 (1-s) \langle H(x_i) H^{-1}(x_i) \nabla f(x_i), H^{-1}(x_i)\nabla f(x_i) \rangle ds\\ &= -\frac{1}{2} \langle \nabla f(x_i), H^{-1}(x_i)\nabla f(x_i) \rangle - \int_0^1 (1-s) \langle H^{-1}(x_i) \nabla f(x_i), H(x_i) H^{-1}(x_i)\nabla f(x_i) \rangle ds\\ \end{align} \tag{4}\]Substitue (4) to (3), then the right term of the equation is
\[\begin{align} &-\frac{1}{2} \langle \nabla f(x_i), H^{-1}(x_i)\nabla f(x_i) \rangle + \alpha \langle \nabla f(x_i), H^{-1}(x_i)\nabla f(x_i) \rangle \\ &+ \int_0^1(1-s) \langle H^{-1}(x_i)\nabla f(x_i), \left( H(x_i + s h_i) - H(x_i) \right) H^{-1} \nabla f(x_i) \rangle ds \\ \end{align} \tag{5}\]Since $\alpha \in (0, \frac{1}{2})$, and $m < H \leq M$
\[\begin{align} (5) &= -(\frac{1}{2} - \alpha) \langle \nabla f(x_i), H^{-1}(x_i)\nabla f(x_i) \rangle + \int_0^1(1-s) \langle h_i, ( H(x_i + s h_i) - H(x_i)) h_i\rangle ds \\ &\leq -(\frac{1}{2} - \alpha) \frac{1}{M} \| \nabla f(x_i) \|^2 + \int_0^1(1-s) \| H^{-1}(x_i) \|^2 \| \nabla f(x_i) \|^2 \| H(x_i + s h_i) - H(x_i) \|^2 ds \\ &\leq -(\frac{1}{2} - \alpha) \frac{1}{M} \| \nabla f(x_i) \|^2 + \int_0^1(1-s) \| H^{-1}(x_i) \|^2 \| \nabla f(x_i) \|^2 \cdot L \cdot s \| h_i \| ds \\ &\leq -(\frac{1}{2} - \alpha) \frac{1}{M} \| \nabla f(x_i) \|^2 + \int_0^1s(1-s) ds \cdot L \cdot \frac{\| \nabla f(x_i) \|^3}{m^3} \;\;\;\;\;\; \because \|H^{-1}(x_i) \| < \frac{1}{m} \\ &\leq \| \nabla f(x_i) \|^2 \left( -\frac{1}{M}(\frac{1}{2} - \alpha) + \frac{L}{6m^3} \| \nabla f(x_i) \| \right) \end{align} \tag{6}\]Since $\nabla f(x_i) \rightarrow \nabla f(\hat{x}) = 0$ 에서 it is possible to get a $i_0$ such that
\[\| \nabla f(x_i) \| \leq \frac{6m^3}{L M}(\frac{1}{2} - \alpha).\]It implies that
\[\exists i_0 \in \mathbb{N} \;\;\text{ such that } f(x_i + h_i) = f(x_i) - \alpha \langle \nabla f(x_i), h_i \rangle \leq 0 \;\;\forall i_0 \geq i\]식 (6)에서 Armijo -Newton Method는 local minima에 Quadratically converge 함을 ( $| \nabla f(x_i) |^2$ 때문에) 알 수 있다.
이후의 증명은 결국 Local Newton Method의 그것과 같다.
Newton Method의 단점
$h_i = -H^{-1}(x_i) \nabla f(x_i) $ 에서
- Does $H^{-1}(x_i)$ exists for any $x_i$
- Should we compute $H^{-1}$, and $\nabla f(x_i)$
Solution
Let $g_i \equiv \nabla f(x_i)$ ve applied to the update rule $ x_{i+1} = x_i - \alpha_i M_i g_i$ for some matrix $M_i$. Consider a Taylor expansion of $f(\cdot)$ at $x = x_i$
\[f(x_{i+1}) = f(x_i) + \langle \nabla f(x_i), x_{i+1} - x_i \rangle + O(|x_{i+1} - x_i|^2) \\ \Rightarrow f(x_{i+1}) - f(x_i) = \langle g_i -\alpha_i M_i g_i \rangle + O(|x_{i+1} - x_i|^2) < 0\]위 식이 성립하기 위한 조건은 $M_i$ 가 positive definite 이어야 한다.
Let $M_i = I$ then $x_{i+1} = x_i - \alpha_i g_i$ is converged linearly. 이것을 Armijo-Newton에 결합시키면 Let
\[M_i = (\varepsilon_i I + H(x_i))^{-1}\]- 그러면 어떻게 $\varepsilon_i$를 잡을 것인가.
- pick any $\delta > 0$, $\delta \geq \varepsilon_i + \lambda_i H(x_i)$ 되도록 잡는다. ($\lambda_i$ 또 무엇?)
Final characters are always wrap up with the below sentence.
- It is Dummy characters for editing and blogging.
Comments