앞 post에 있는 Nonlinear Optimization with Quantization [1] 의 후속편이다.
NLP_Quantization01.ipynb 을 기본으로 Armijo Rule, General Conjugate Descent, Quasi Newton 방법을 모두 구현해 본다. 간단하게 각 알고리즘을 비교해 보기 위하여 대체로 앞 부분은 Library로 모아본다.
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
import pandas as pd
import seaborn as sns
import numpy as np
import sys
import argparse
# Set Search Point
Initial_point = np.array([-0.25548896, 0.0705816])
X = np.array(Initial_point, dtype=np.float64) # Main Training Parameter
# For evaluation of Armijo'rule
alpha = 0.5
beta = 0.612
Initial_StepSize = 0.9
# For Conjugate Gradient
CGmethod = 0 # 0 : Polak - Riebel
# 1 : Fletcher-Reeves
# Quasi Newton
AlgorithmWeight = 0.0 # Weight of DFP if zero, it means that BFGS
# Line Search (Golden Search)
F = 0.618
LimitofLineSearch = 20
# Algorithm Control
stop_condition = 0.00003
SearchAlgorithm = 2 # 0 : General Gradient
# 1 : Conjugate Gradient
# 2 : Quasi Newton
StepSizeRule = 1 # 0 : Constant
# 1 : Armijo Rule
# 2 : Line Search
ArmijoDebugFreq = 10
Constant_StepSize = 0.002
training_steps = 1000 # Maximum Number of Training Steps
debugfrequency = 10 # print the information per debugfrequency for each step
bArgumentInput = False
Argument Parsig
Argument Parsing의 경우 Google colaboratory 에서는 잘 수행되지 않으나, 이후 python 단독으로 구동시킬 때나 혹은 python -> EXE에서 사용할 수 있어야 하므로 다음 코드의 형태로 남겨 놓는다.
Argument의 입력이 없는 경우
예를 들어 Quasi Newton (-a 4)를 선택했는데, Qausi Newton을 위한 Weight 값 (즉, DFP알고리즘을 BGFS에 비하여 얼마나 적용할지에 대하여 ) 을 선택하지 않고 system default 값을 사용한다고 하면 args,weight == None 이므로 이러한 경우를 피하면 된다.
- Python Program의 실행 성을 본다면 Argumet를 적극 이용하는 것이 좋다.
strAlgorithmName = ['General Gradient', 'Conjugate Gradient', 'Quasi Newton']
if bArgumentInput :
# parse command line arguments
Algorithm_Help_String = "Search Algorithm \n [0] General Gradient with constant gradient \n [1] General Conjugate Gradient with Armijo \n" \
+ "[2] Conjugate Gradient with Polak - Riebel \n [3] Conjugate Gradient with Fletcher-Reeves \n [4] Quasi Newton"
parser = argparse.ArgumentParser(
description="Nonlinear Optimization")
parser.add_argument('-a', '--algorithm', help= Algorithm_Help_String, default= SearchAlgorithm * 2, type=int)
parser.add_argument('-w', '--weight', help="Weight for Quasi Newton WEIGHT x (DFP) + (1 - WEIGHT)(BFGS). The lower limit is 0.0 and highest limit is 1.0", type=float, default= AlgorithmWeight)
parser.add_argument('-df', '--debugfreq', help="Debugging Frequency. Ir means that each time of (time mod df)==0 prints out the debugginf infot", type=int, default=debugfrequency)
parser.add_argument('-s', '--stepsize', help="Stepsize Rule [0] Constant [1] Armijo Rule [2] Line Search", type=int, default=StepSizeRule )
args = parser.parse_args()
# Set Algorithm Type : It should be modified when a new algorithm is added
SearchAlgorithm = args.algorithm >> 1
CGmethod = ((args.algorithm & 2)>>1) & (args.algorithm & 1)
AlgorithmWeight = np.clip(args.weight, 0.0, 1.0)
debugfrequency = args.debugfreq
StepSizeRule = args.stepsize
Library
주요 라이브러라 파일들은 여기에 만들어 놓는다.
Inference
Inference는 로젠브록 함수(Rosenbrock function)이며 다음의 함수식 이다. \(f ( x , y ) = ( a − x )^2 + b ( y − x^2 )^2\)
전역최소값은 $f ( x = a , y = a^2 ) = 0$ 이다. $a = 1 , b = 100$ 을 대입해 사용한다. \(f ( x , y ) = ( 1 − x )^2 + 100 ( y − x^2 )^2\)
이것의 Gradient는 다음과 같다.
\[\nabla f(x,y) = \left( \frac{\partial f}{\partial x}, \; \frac{\partial f}{\partial y} \right)^T = \begin{pmatrix} -2(a-x) -4bx(y - x^2) \\ 2b(y - x^2) \end{pmatrix}\]Stepsize evaluated by Armijo’s rule
Armijo Rule에 따른 Step size 계산시 사용된다. Gradient Descent 이므로 (-) 기호가 되어야 해서 Lecture 에서는 $f(x_i + \beta^k h_i)$ 로 되어 있는 것을 (물론 그 위에 $h_i = -\nabla f(x_i)$ 로 정의 되어 있다.) $f(x_i - \beta^k h_i)$로 수정한다.
\[\lambda_i = \lambda(x_i) \triangleq \arg \max_{k \in \mathbb{N}} \{ \beta^k | f(x_i - \beta^k h_i) - f(x_i) \leq -\beta^k \cdot \alpha \| \nabla f(x_i) \|^2 \}\]-
위에서 정의된 Armijo Rule 을 개량할 필요성이 있다. 가장 큰 부분은 $\alpha$ 에대한 부분인데, 이 항이 고정된 값으로 되어 있다. 만일, 이 값을 조금씩 작게 만들 수 있다면 보다 적응적으로 움직이는 알고리즘이 될 것이다.
-
예를 들어 현재 코드에서는 만일 Armijo Rule이 빠르게 $\lambda = \beta^k$ 를 찾지 못한다면, Chk_freq를 보고 $\alpha$ 값을 적절히줄이는 방식으로 구성하였다. 즉, $\alpha<0$ 이므로 $\alpha_{\text{next}} = \alpha^k$ 이 되도록 구성하였다.
- 하지만 그렇게 효과가 있지는 않다. 보다 적절한 방법이 필요할 것으로 생각된다.
fa = 1
fb = 100
def inference(X):
# compute inference model over data X and return the result
Z = (fa - X[0])**2 + fb * (X[1] - X[0]**2)**2 #Armijo Rule을 위한 Evaluation (numPy)
return Z
def Calculate_Gradient(npX):
g_0 = -2 * (fa - npX[0]) - 4 * fb * (npX[1] - npX[0]**2) * npX[0]
g_1 = 2 * fb * (npX[1] - npX[0]**2)
g = np.array([g_0, g_1], dtype = np.float64)
return g
def Armijo_Lambda(np_x, np_g, np_h, _cost, bTestCase):
# bTestCase : [True] Armijo Rule, [False] Constant
if bTestCase:
chk_freq = ArmijoDebugFreq # Set Debugging Frequency
beta_k = Initial_StepSize
grad = alpha * np.inner(np_g, np_g) # \beta^0
chk_cnt = 0
while True:
xn = np_x - beta_k * np_h # x_i - \beta^k h_i
Phi = inference(xn) - _cost # f(x_i + \beta^k h_i) - f(x_i)
Psi = - beta_k * grad # -beta^k \cdot \alpha \| \nabla f(x_i) \|^2
if Phi > Psi:
beta_k = beta_k * beta
chk_cnt = chk_cnt + 1
if chk_cnt % chk_freq == 0:
grad = grad * alpha # := alpha^k
nr_grad = np.linalg.norm(grad)
print("Armijo Info count:", "%4d" %chk_cnt, "beta:", "%4.8f" %beta_k, "alpha * |grad| :", "%4.8f" %nr_grad)
else:
Lambda = beta_k
break
else:
Lambda = Constant_StepSize
return Lambda
def Description_of_Object_Function(np_X, np_Cost):
x = np.arange(-2.0, 3.0, 0.05)
y = np.arange(-2.0, 3.0, 0.05)
X, Y = np.meshgrid(x, y)
Z = inference(np.array([X, Y]))
return X, Y, Z
def plot_result(X, Y, Z, np_X, np_Cost):
fig = plt.figure()
ax = fig.gca(projection='3d') # 3d axes instance
surf = ax.plot_surface(X, Y, Z, # data values (2D Arryas)
rstride=2, # row step size
cstride=2, # column step size
cmap=cm.RdPu, # colour map
linewidth=1, # wireframe line width
antialiased=True)
# Point of X
ax.plot(np_X[:,0], np_X[:,1], np_Cost, 'b.')
ax.set_title('Hyperbolic Paraboloid') # title
ax.set_xlabel('x label') # x label
ax.set_ylabel('y label') # y label
ax.set_zlabel('z label') # z label
fig.colorbar(surf, shrink=0.5, aspect=5) # colour bar
ax.view_init(elev=15,azim=70) # elevation & angle
ax.dist=8 # distance from the plot
plt.show()
return
def print_process(step, epsilon, prev_cost, current_cost, np_lambda, X, lRecord, printfreq = 10):
#Programming Result
if (step % printfreq == 0):
print("step: ", "%3d" %step, "epsilon: ", "%4.8f" %epsilon, "prev_cost: ", "%4.8f" %prev_cost, "current_cost: ", "%4.8f" %current_cost, "np_lambda :", "%4.8f" %np_lambda, "X ", X)
rEpsilon = lRecord[0]
rCost = lRecord[1]
rX = lRecord[2]
rLambda = lRecord[3]
rEpsilon.append(epsilon)
rCost.append(current_cost)
rLambda.append(np_lambda)
rX.append(X)
return [rEpsilon, rCost, rX, rLambda]
Line Search : Golden Search
Armijo Rule 이외에, Quasi Newton의 경우, Armijo Rule 보다 Line Search에 의해 Hessian의 기능을 극대화 (즉, 2차 함수 근사화) 시킬 필요성이 있다.
Golden Search에 의해 Gradient Descent 혹은 $-H^{-1} \nabla f(x)$ Line 에서의 값을 최소화 시키는 점을 찾아 그 점으로 움직이도록 Step Size를 결정하도록 한다.
함수는 2개로 하나는 Line Search 로 $x_{n+1}$을 찾고, 나머지 하나는 $\alpha_t $를 찾는 것이다.
일반적인 경우 Line Search 는 Length $L = b_i - a_i$에 대하여 \(\begin{align} a_i &= a + (1 - F) \cdot L \\ b_i &= b - (1 - F) \cdot L \end{align}\) 이나, $a_0 = x, b_0 = x - h$ 로 보면 $L$은 $-h$ 가 되므로
\[\begin{align} a_i &= x + (1 - F) (-h) = x - (1 - F) h \\ b_i &= x - h - (1 - F)(-h) = x - h + h -Fh = x - Fh \end{align}\]Line Search에서의 Stop Condition 은 $| a_i - b_i | < \epsilon$ 혹은 최대 Iteration=20 으로 하였다.
Calculate StepSize
다음과 같이 주어진 Search Alorithm에서
\[x_{i+1} = x_i - \lambda h_i\]$\lambda$는 다음과 같이 구할 수 있다.
\[\begin{align} \lambda h_i &= x_i - x_{i+1} \\ \lambda \langle h_i, h_i \rangle &= (x_i - x_{i+1}) \cdot h_i \\ \therefore \lambda &= \frac{1}{\langle h_i, h_i \rangle}(x_i - x_{i+1}) \cdot h_i \end{align}\]def LineSearch(x, h, debug=True):
a = x
b = x - h
chk_cnt = 0
while True:
L = b - a
ai = a + (1 - F) * L
bi = b - (1 - F) * L
Pai = inference(ai)
Pbi = inference(bi)
if Pbi <= Pai:
a = ai
else:
b = bi
if debug:
print("[Step:", chk_cnt, "]", "a:", a, " ai:", ai, "f(ai)=", Pai, " b:", b, " bi:", bi, "f(bi)=", Pbi)
_dLenth = ai - bi
_epsilon = np.linalg.norm(_dLenth)
bStopCondition = (chk_cnt >= LimitofLineSearch) or (_epsilon < stop_condition)
if bStopCondition :
print("[Step:", chk_cnt, "]", "a:", a, " ai:", ai, "f(ai)=", Pai, " b:", b, " bi:", bi, "f(bi)=", Pbi)
break
chk_cnt = chk_cnt + 1
if Pbi <= Pai:
xn = bi
else:
xn = ai
return xn
def CalulateStepsize(x, xn, h):
test_01 = np.asscalar(np.dot((x - xn), h))
test_02 = np.asscalar(np.dot(h, h))
Lambda = test_01/test_02
return Lambda
Initialization of Main Routine
본 함수 시작전의 부분을 이곳에 놓는다.
일부 알고리즘은 $X_0$가 필요한 경우 이곳에서 관련 연산을 미리 수행한다.
#=================================================================
# Main Routine
#=================================================================
# For record a simulation
rEpsilon = []
rCost = []
rX = []
rLambda = []
lRecord = [rEpsilon, rCost, rX, rLambda]
#Description_of_Object_Function()
prev_cost = inference(X)
gr = Calculate_Gradient(X)
gr_n = np.zeros(np.shape(X), dtype= np.float64)
h = gr
B = np.eye(np.shape(X)[0], dtype=np.float64)
print("Initial f(x):", prev_cost, "at:", X, "Gradient:", gr, "B:", B)
Main Search Routine
현재, For 문으로 구성되어 있는 부분 아래 부분이다. 해당 부분은 알고리즘에 따라 나누어 질 예정이다.
Stop Condition을 안에 넣을 것인가 고민하다가 일단 넣기로 하였다.
해당 코드는 일단 함수화 시켜야 할 필요성이 있다.
정상적으로 출력이 되는지를 모두 테스트 한 후, 코드를 변경한다.
Conjugate Gradient
Conjugate Gradient의 경우 다음 두 가지 방법 중 하나를 선택한다.
- Polak - Riebel Formula
- Fletcher-Reeves Formula
- Since for the quadratic case, $\langle g_{i+1}, g_{i} \rangle = 0$, that results can be extended. \(r_i = - \frac{\| g_{i+1} \|^2}{\| g_i \|^2}\)
원래는 $r_i$ 값에 마이너스 값이 붙어야 하나, 양쪽 방법 모두 마이너스를 붙여서 사용하기 때문에 둘 다 플러스로 놓고 $h_i$ Update시 마이너스 방향으로 update 하는 방식으로 바꾸었다.
Quasi Newton
Quasi Newton 법은 원래 $x_{i+1} = x_i - \lambda_i H_i^{-1} \nabla f(x_i)$ 와 같이 Hessian의 Inverse를 필요로 하는 Newton-Rapson 방법에서 Hessian의 Inverse를 Feasible한 가정을 두고 (예; Symmetry 조건) Update 가능한 방식으로 Hessian을 구하는 방법. 즉, $\beta^{-1}(x_i) = H(x_i)$ 로 놓고 Matrix Inverse Lemma를 사용하여 Update 하는 방식
- DFP Method
- BFGS Method
Let $p_i = \frac{1}{\langle \Delta x_i, \Delta g_i \rangle} \in \mathbf{R}$ . Since$\Delta g_i^T \beta_i \Delta g_i \in \mathbf{R}$, $(\Delta g_i^T \beta_i \Delta g_i )\Delta x \Delta x^T = \Delta x \Delta g_i^T \beta_i \Delta g_i \Delta x^T$ . Therefore,
\[\begin{aligned} \beta_{i+1}^{BFGS} &= \beta_i +p_i (1 + p_i \Delta g_i^T \beta_i \Delta g_i ) \Delta x_i \Delta x_i^T - p_i (\beta_i \Delta g_i \Delta x_i^T + \Delta x_i \Delta g_i^T \beta_i) \\ &= \beta_i + p_i (\Delta x_i \Delta x_i^T + p_i \Delta x_i \Delta g_i^T \beta_i \Delta g_i \Delta x_i^T) - p_i (\beta_i \Delta g_i \Delta x_i^T + \Delta x_i \Delta g_i^T \beta_i) \\ &= \beta_i - p_i (\beta_i \Delta g_i \Delta x_i^T + \Delta x_i \Delta g_i^T \beta_i) + p_i^2 \Delta x_i \Delta g_i^T \beta_i \Delta g_i \Delta x_i^T + p_i \Delta x_i \Delta x_i^T \\ &= (I - p_i \Delta x_i \Delta g_i^T) \beta_i (I - p_i \Delta g_i \Delta x_i^T) + p_i \Delta x_i \Delta x_i^T \end{aligned}\]In may text books, $y_i : = \Delta g_i = \nabla f(x_{i+1}) - \nabla f(x_i)$, and $s_i := \Delta x_{i+1} - \Delta x_i$, so that I re-write the above equation as follows:
\[\beta_{i+1}^{BFGS} = (I - p_i s_i y_i^T) \beta_i (I - p_i y_i s_i^T) + p_i s_i s_i^T\]- L-BFGS and Other Methods
Since it consumes a lot of computational power to implement the BFGS algorithm with C/C++ or FORTRAN arised from the computation of matrix, the Limited-memory BFGS (L-BFGS) was developed. However, now a days, the implementation of BFGS with Python does not need a such a recursive based fast algorithm, since Python supports effective matrix or vector computation by parallel processing based on SIMD(Single Instruction Mutiple Data) or GPU.
Consequently, I don’t develope the L-BFGS algorithm with Python, however I will write the developing procedure of L-BFGS algorithm in another post.
Python 구현상의 문제점
Matrix 연산이기 때문에 Python에서 처음부터 $x \in \mathbf{R}^2$ 에 대하여 [[x_1]\ [x_2]\ … [x_n]] 과 같이 구성되도록 하여야 한다. 이때문에, Python code상에 Matlab 에서는 볼 수 없는 matrix 연산 명령이 나타나게 된다.
#=================================================================
# Search Routine
#=================================================================
for step in range(training_steps):
# Main Search Rule
if StepSizeRule == 0:
lm = Armijo_Lambda(X, gr, h, prev_cost, False)
elif StepSizeRule == 1:
lm = Armijo_Lambda(X, gr, h, prev_cost, True)
else:
Xmin = LineSearch(X, h, False)
lm = CalulateStepsize(X, Xmin, h)
Xn = X - lm * h
gr_n = Calculate_Gradient(Xn)
if SearchAlgorithm == 1:
# Comjugate Gradient
if CGmethod == 0:
rc = np.inner(gr_n - gr, gr_n)/np.inner(gr, gr)
else:
rc = np.inner(gr_n, gr_n)/np.inner(gr, gr)
gr = gr_n
h = gr_n - rc * h
elif SearchAlgorithm == 2:
# Quasi Newton
basicDim = (np.size(X), 1)
dX = np.reshape(Xn - X, basicDim) # General 2x1 Vector (tuple)
dG = np.reshape(gr_n - gr,basicDim)
# DFP Method
BdG = np.dot(B, dG) # B : 2x2 to 2x1
dXdXt = np.dot(dX, dX.T) # 2x2 Matrix
BdGBdGt = np.dot(BdG, BdG.T) # 2x2 Matrix
test_0 = np.asscalar(np.dot(dX.T, gr))
test_1 = np.asscalar(np.dot(BdG.T, dG))
Bn_DFP = B + (dXdXt/test_0 ) - (BdGBdGt/test_1)
# BFGS Method
dGdGt = np.dot(dG, dG.T)
test_0 = np.asscalar(np.dot(dX.T, dG))
test_1 = np.asscalar(np.dot(dG.T, np.dot(B, dG))) + test_0
test_2 = np.dot(B, np.dot(dG, dX.T)) + np.dot(np.dot(dX, dG.T), B)
Bn_BFGS= B + (test_1/test_0) * (dXdXt/test_0) - (test_2/test_0)
_pr = AlgorithmWeight
B = _pr * Bn_DFP + (1 - _pr)*Bn_BFGS
gr = gr_n
h = np.matmul(B, gr_n)
else:
# Armijo Gradient
gr = gr_n
h = gr_n
# Evaluation of epsilon to check Stop Condition
current_cost = inference(Xn)
epsilon = prev_cost - current_cost
# Programming Result
[rEpsilon, rCost, rX, rLambda] = print_process(step, epsilon, prev_cost, current_cost, lm, Xn, lRecord, debugfrequency)
# Update Search point and Check Process Stop
prev_cost = current_cost
X = Xn
if (step > 0) & (epsilon < stop_condition) : break
Final Routine
이 부분은 For 문 혹은 While 문이 끝나는 경우 들어가는 부분이다.
알고리즘 수행 후 최종 결과가 나타나는 부분이다.
#=================================================================
# Final Routine
#=================================================================
Algorithm_Info_buf = ["Armijo ", "Constant Step Size "]
ConjugateGradientInfo = ["Polak-Riebel", "Fletcher-Reeves"]
print("")
print("=========== Final Result ===========")
print("Algorithm :", strAlgorithmName[SearchAlgorithm])
BufIdx = 1
if bArmijo_On: BufIdx = 0
print(" Step Size Rule :", Algorithm_Info_buf[BufIdx])
if SearchAlgorithm == 1:
print(" Conjugate Gradient Method:", ConjugateGradientInfo[CGmethod])
if SearchAlgorithm == 2:
print(" Algorithm Weight [DFP] :", _pr, "[BFGS] : ", (1 - _pr))
print("====================================")
print('step: %3d epsilon: %4.8f prev_cost: %4.8f current_cost: %4.8f ' %(step, epsilon, prev_cost, current_cost), "lambda", lm, "X", X)
print("====================================")
# Data Management
time_index = range(step+1)
np_rX = np.array(rX)
np_Cost = np.array(rCost)
X, Y, Z = Description_of_Object_Function(np_rX, np_Cost)
# plot dub-figure (trend of epsilon, cost, Lmabda and trace of X)
plt.subplot(221)
plt.plot(time_index, rEpsilon, 'b')
plt.ylabel('Epsilon')
plt.legend
plt.subplot(222)
plt.plot(time_index, rCost, 'r')
plt.ylabel('Cost')
plt.legend
plt.subplot(223)
plt.plot(time_index, rLambda, 'b')
plt.ylabel('Lambda')
plt.legend
plt.subplot(224)
levels = [2e-8, 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048]
plt.contour(X, Y, Z, levels)
plt.plot(np_rX[:,0], np_rX[:,1], 'b')
plt.show()
# 3D plot of Object function and Distribution of X
plot_result(X, Y, Z, np_rX, np_Cost)
다음은 Quasi Newton으로 수행한 결과이다. Armijo Rile 대신 Line Search 방식을 사용하였다.
=========== Final Result ===========
Algorithm : Quasi Newton
Step Size Rule : Line Search
Algorithm Weight [DFP] : 0.0 [BFGS] : 1.0
====================================
step: 19 epsilon: 0.00002339 prev_cost: 0.00000066 current_cost: 0.00000066 lambda 0.9918722345253849 X [0.99938116 0.99871038]
====================================
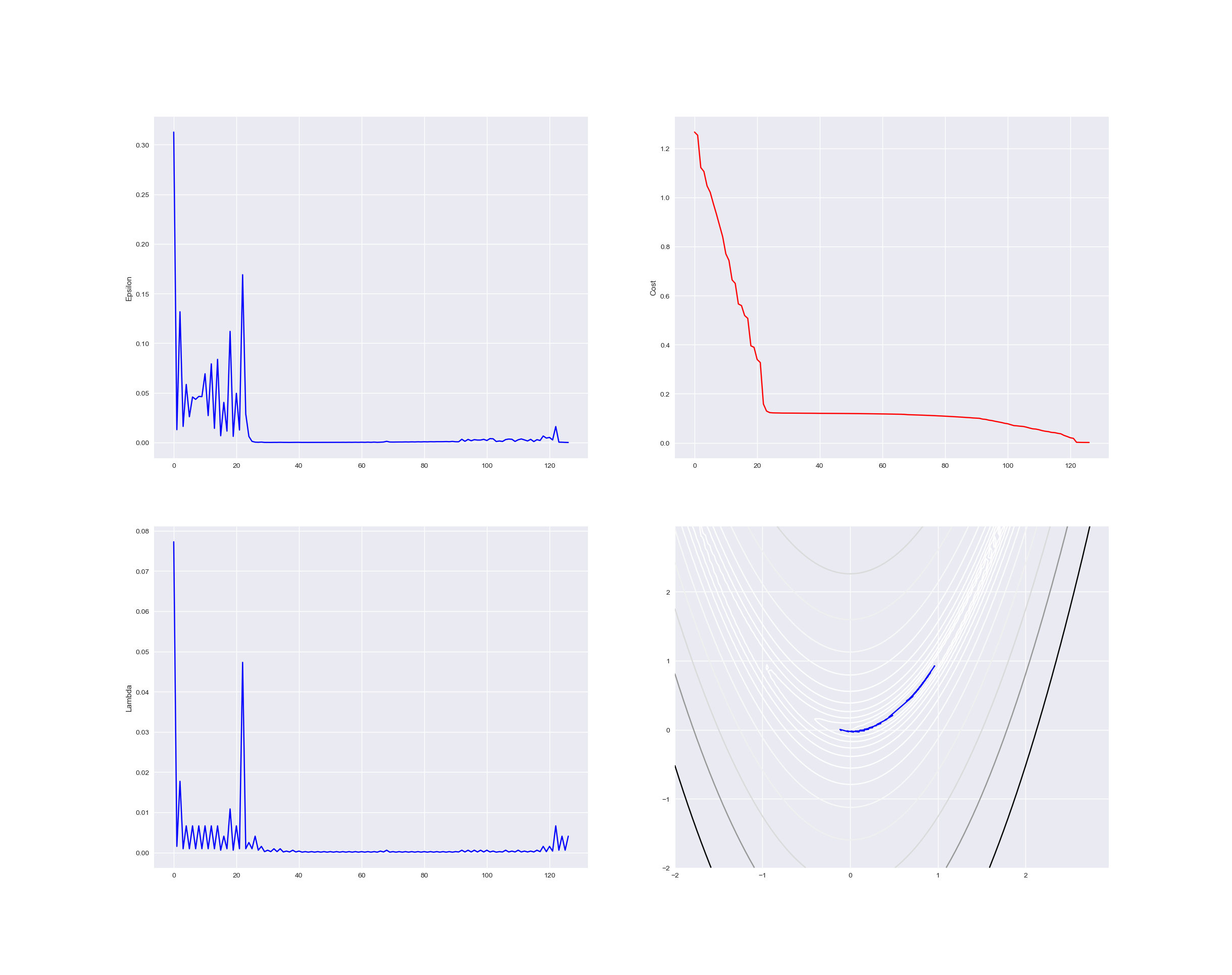
다음은 Rosenbrook 함수에서 Conjugate Gradient Descent 중 Fletcher-Reeves 방식으로 최적화를 수행했을 때의 결과이다. 좌측부터 $\epsilon = \text{Previous Cost} - \text{Current Cost}$, Cost, Step Size, Search Point가 움직인 경로 (Initial Point [-0.25548896, 0.0705816] 에서 출발한 경로) 이다.
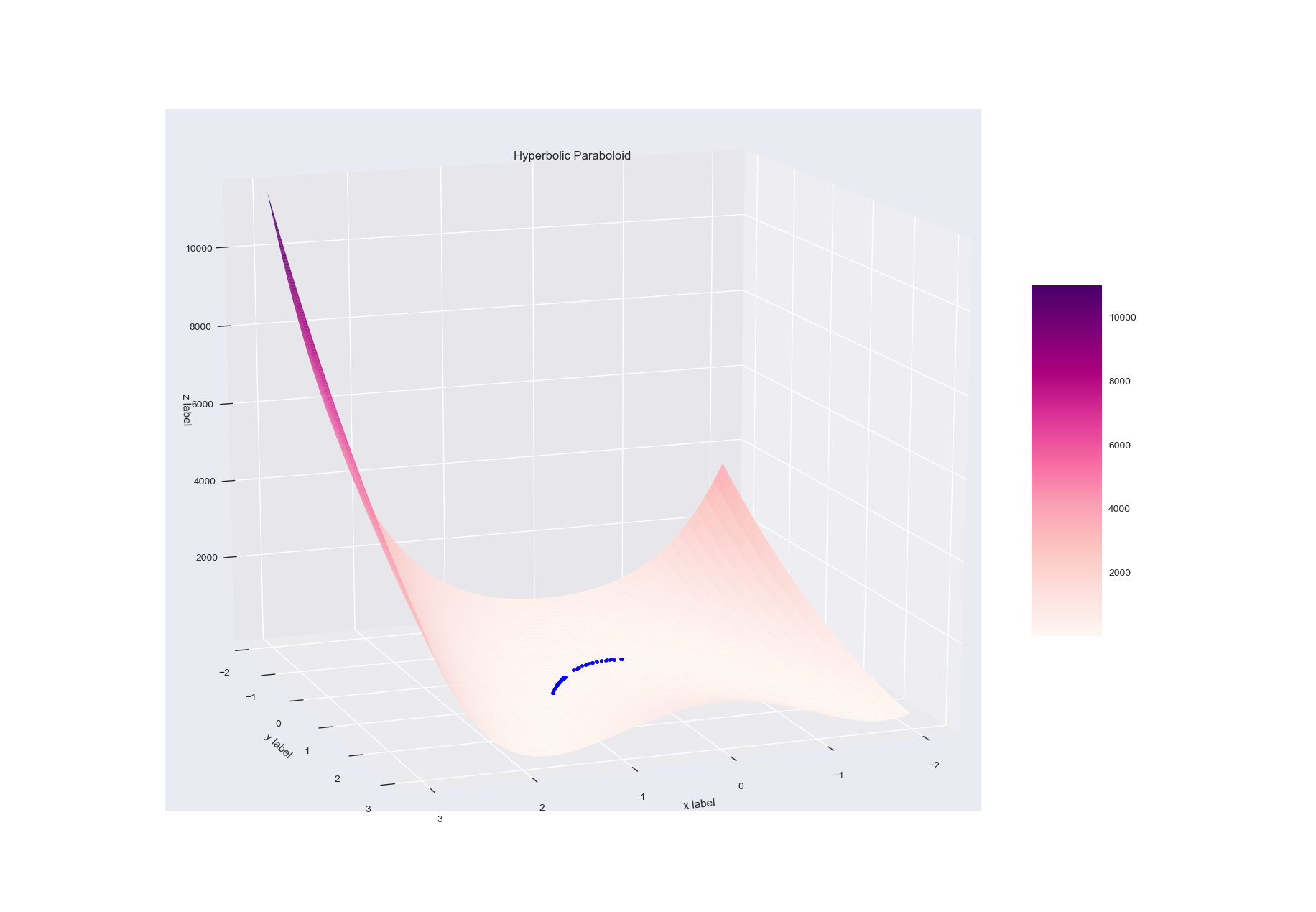
다음은 3차원으로 도시된 Rosenbrook 함수에서 움직인 경로를 도시한 것이다.
본 프로그램의 사용
본 포스트에 나와 있는 코드를 단순히 이어 붙여서 사용해도 된다. 기본적인 사용법은 -h 혹은 –help 옵션을 통해 알 수 있다.
보다 진보적인 방법은 본 프로그램에서 Search Algorithm에 해당하는 부분을 Class 객체화 시켜서 사용하여 기ㅖ학습 등에 적용하는 것이다. 해당 사항에 대해서는 추후에 다시 언급하도록 한다.
Comments